题目内容
如图,已知在正四面体ABCD中,O为A在BCD面内的射影,M为AO中点,求证MB、MC、MD两两垂直.

答案:
解析:
解析:
|
证明 设正四面体棱长为A.由ABCD为正四面体,知O为△BCD中心.延长BO,交CD于E,连结ME.BE= 在Rt△MBO中,MB= ∵ ∴ BM⊥ME. 又由三垂线定理,知BM⊥CD,ME∩CD=E,故BM⊥平面MCD.又 同理可证MC⊥MD,MC⊥MB.故MB、MC、MD两两垂直. 本题还可在求出MB= ∵ ∴MB⊥MC. 同理MB⊥MD,MD⊥MC. ∴MB、MC、MD两两垂直. 通过“计算”来证明线线垂直是此例证明的特点. |

练习册系列答案
相关题目
 a,OE=
a,OE=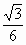 a,BO=
a,BO=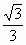 A.在Rt△AOB中,AO=
A.在Rt△AOB中,AO=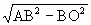 =
=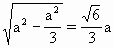 ,故MO=
,故MO=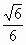 a.
a.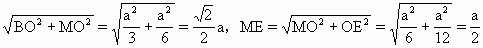 .
.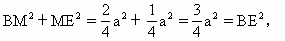
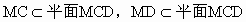 ,故BM⊥MC,BM⊥MD.
,故BM⊥MC,BM⊥MD. a后,同理可知MC=MD=
a后,同理可知MC=MD=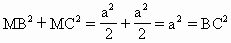 ,
, 如图,已知正四面体ABCD的棱长为3cm.
如图,已知正四面体ABCD的棱长为3cm.
