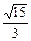题目内容
如图(1),矩形ABCD中,AB=2AD=2a,E为DC的中点,现将△ADE沿AE折起,使平面ADE⊥平面ABCE,如图(2),F为AE的中点.
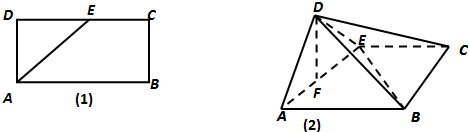
(1)求证:DF⊥平面ABCE,
(2)求四棱锥D-ABCE的体积;
(3)求证:BE⊥AD.
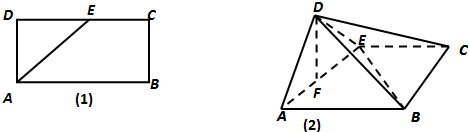
(1)求证:DF⊥平面ABCE,
(2)求四棱锥D-ABCE的体积;
(3)求证:BE⊥AD.
分析:(1)利用△ADE为等腰直角三角形,F是中点,可得DF⊥AE,再根据面面垂直的性质可证DF⊥平面ABCE;
(2)由(1)知:DF为四棱锥D-ABCE的高,DF=
a,根据底面为直角梯形求出底面面积,代入棱锥的体积公式计算;
(3)在△ABE中,求出BE、AE的长,利用勾股定理可证AE⊥BE,从而证明BE⊥平面ADE,由线面垂直的性质可证BE⊥AD.
(2)由(1)知:DF为四棱锥D-ABCE的高,DF=
| ||
| 2 |
(3)在△ABE中,求出BE、AE的长,利用勾股定理可证AE⊥BE,从而证明BE⊥平面ADE,由线面垂直的性质可证BE⊥AD.
解答:解: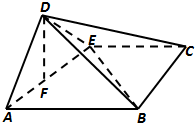 (1)证明:∵△ADE为等腰直角三角形,F是中点,∴DF⊥AE,
(1)证明:∵△ADE为等腰直角三角形,F是中点,∴DF⊥AE,
∵平面ADE⊥平面ABCE,DF?平面ADE,平面ADE∩平面ABCE=AE,
∴DF⊥平面ABCE;
(2)由(1)知:DF为四棱锥D-ABCE的高,DF=
a,
根据底面为直角梯形其面积为
×BC=
×a=
a2;
∴VD-ABCE=
SABCE•DF=
•
a2•
a=
a3;
(2)证明:由(1)知:DF⊥平面ABCE,BE?平面ABCE,
∴DF⊥BE,
又AE=BE=
a,AB=2a,
∴AE2+BE2=AB2,∴AE⊥BE,
∵AE∩DF=F,AE,DF?平面ADE,
∴BE⊥平面ADE,从而有BE⊥AD.
 (1)证明:∵△ADE为等腰直角三角形,F是中点,∴DF⊥AE,
(1)证明:∵△ADE为等腰直角三角形,F是中点,∴DF⊥AE,∵平面ADE⊥平面ABCE,DF?平面ADE,平面ADE∩平面ABCE=AE,
∴DF⊥平面ABCE;
(2)由(1)知:DF为四棱锥D-ABCE的高,DF=
| ||
| 2 |
根据底面为直角梯形其面积为
| AB+CE |
| 2 |
| 2a+a |
| 2 |
| 3 |
| 2 |
∴VD-ABCE=
| 1 |
| 3 |
| 1 |
| 3 |
| 3 |
| 2 |
| ||
| 2 |
| ||
| 4 |
(2)证明:由(1)知:DF⊥平面ABCE,BE?平面ABCE,
∴DF⊥BE,
又AE=BE=
| 2 |
∴AE2+BE2=AB2,∴AE⊥BE,
∵AE∩DF=F,AE,DF?平面ADE,
∴BE⊥平面ADE,从而有BE⊥AD.
点评:本题考查了线面垂直的判定与性质,考查了棱锥的体积公式,考查了学生的推理论证能力,属于中档题.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
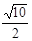 (B)
(B) (C)
(C)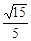 (D)
(D)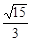

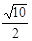 (B)
(B)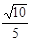 (C)
(C)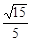 (D)
(D)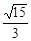
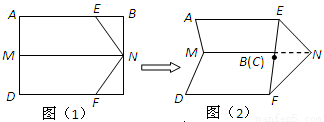
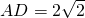 ,MN分别为AD和BC的中点,对角线BD与MN交于O点,沿MN把矩形ABNM折起,使平面ABNM与平面MNCD所成角为60°,如图 (2).
,MN分别为AD和BC的中点,对角线BD与MN交于O点,沿MN把矩形ABNM折起,使平面ABNM与平面MNCD所成角为60°,如图 (2).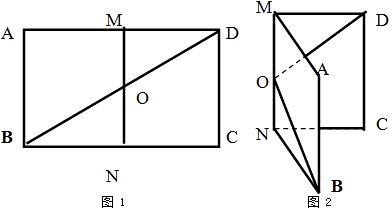
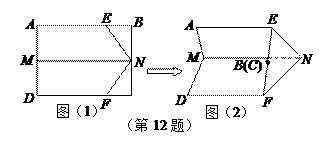
 (B)
(B)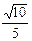 (C)
(C)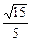 (D)
(D)