题目内容
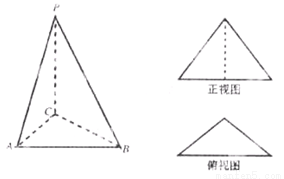
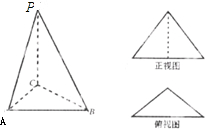
某三棱锥P-ABC的正视图为如图所示边长为2的正三角形，俯视图为等腰直角三角形，则三棱锥的表面积是_______.
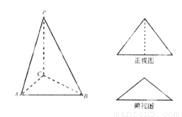
【答案】
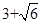
【解析】
试题分析：由俯视图是等腰直角三角形知：PC、AC、BC两两相互垂直,且AC=BC.所以三棱锥的高即PC.由正视图是边长为2的正三角形知：高PC=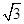
，底边AB=2.所以AC=BC=
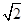，由勾股定理得PA=PB=
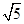.又AB=2，所以三角形PAB中AB边上的高为2.易知底面三角形ABC的面积为1，侧面三角形PAC与PBC的面积均为
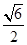，侧面三角形PAB的面积为2.所以三棱锥的表面积为.
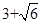考点：三视图与直观图
练习册系列答案
相关题目
（2013•黄冈模拟）某三棱锥P-ABC的正视图为如图所示边长为2的正三角形，俯视图为等腰直角三角形，则三棱锥的表面积是某平行六面体各棱长均为4，在由顶点P出发的三条棱上分别截取PA=1，PB=2，PC=3，则三棱锥P-ABC的体积是原平行六面体体积的（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
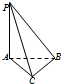已知如图在三棱锥P-ABC中，PA⊥平面ABC，AC⊥BC，PA=AC=BC=1，若三棱锥P-ABC的四个顶点都在某一个球面上，则该球的表面积为（ ）