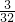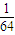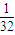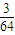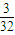题目内容
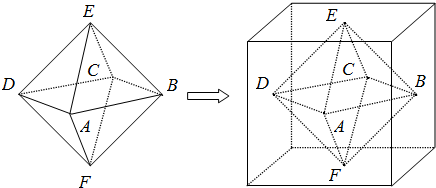
某平行六面体各棱长均为4,在由顶点P出发的三条棱上分别截取PA=1,PB=2,PC=3,则三棱锥P-ABC的体积是原平行六面体体积的( )
A、
| ||
B、
| ||
C、
| ||
D、
|
分析:采用特值法的思想,不妨令此平行六面体为一个正方体,易得其体积为64,再由公式求出三棱锥P-ABC的体积,求它们的比值即可
解答:解:不妨令此平行六面体为一个正方体,易得其体积为64,
∵顶点P出发的三条棱上分别截取PA=1,PB=2,PC=3,
∴三棱锥P-ABC的体积是
×2×
×1×3=1
故三棱锥P-ABC的体积是原平行六面体体积的
故选A
∵顶点P出发的三条棱上分别截取PA=1,PB=2,PC=3,
∴三棱锥P-ABC的体积是
| 1 |
| 3 |
| 1 |
| 2 |
故三棱锥P-ABC的体积是原平行六面体体积的
| 1 |
| 64 |
故选A
点评:本题考查棱柱、棱锥的体积求法,由于本题是一个选择题,符合题意的选项一定符合其特殊情况,这是利用特值法解选择题的理论基础,如此一转化,题目易做,做题时要注意特值法的应用,本题解题的关键是理解平行六面体的几何特征及熟记柱、锥的体积公式

练习册系列答案
 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目