题目内容
已知P(1,cosx),Q(cosx,1),x∈[- ,
, ].
].(1)求向量
 和
和 的夹角θ的余弦用x表示的函数f(x);
的夹角θ的余弦用x表示的函数f(x);(2)求θ的最值.
【答案】分析:(1)求出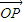 •
•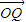 =2cosx,以及|
=2cosx,以及|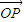 |•|
|•| |,依据题意,写出函数f(x);
|,依据题意,写出函数f(x);
(2)根据(1)函数的表达式,结合x的范围,利用基本不等式以及三角函数的值域,求出θ的最值.
解答:解:(1)∵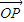 •
•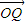 =2cosx,
=2cosx,
|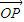 |•|
|•|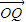 |=1+cos2x,
|=1+cos2x,
∴f(x)=cosθ=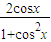 .
.
(2)cosθ=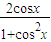 =
=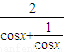 ,
,
x∈[-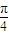 ,
,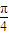 ],cosx∈[
],cosx∈[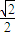 ,1].
,1].
∴2≤cosx+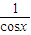 ≤
≤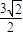 ,
,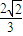 ≤f(x)≤1,即
≤f(x)≤1,即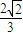 ≤cosθ≤1.
≤cosθ≤1.
∴θmax=arccos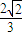 ,θmin=0.
,θmin=0.
点评:本题是基础题,考查三角函数的最值,数量积表示两个向量的夹角,考查计算能力,基本不等式的应用,注意基本不等式的应用条件.
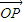 •
•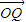 =2cosx,以及|
=2cosx,以及|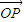 |•|
|•| |,依据题意,写出函数f(x);
|,依据题意,写出函数f(x);(2)根据(1)函数的表达式,结合x的范围,利用基本不等式以及三角函数的值域,求出θ的最值.
解答:解:(1)∵
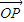 •
•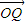 =2cosx,
=2cosx,|
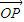 |•|
|•|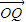 |=1+cos2x,
|=1+cos2x,∴f(x)=cosθ=
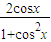 .
.(2)cosθ=
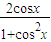 =
=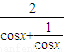 ,
,x∈[-
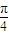 ,
,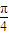 ],cosx∈[
],cosx∈[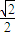 ,1].
,1].∴2≤cosx+
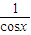 ≤
≤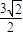 ,
,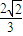 ≤f(x)≤1,即
≤f(x)≤1,即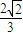 ≤cosθ≤1.
≤cosθ≤1.∴θmax=arccos
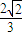 ,θmin=0.
,θmin=0.点评:本题是基础题,考查三角函数的最值,数量积表示两个向量的夹角,考查计算能力,基本不等式的应用,注意基本不等式的应用条件.

练习册系列答案
相关题目
 ,
, 和
和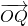 的夹角θ的余弦用x表示的函数f(x);
的夹角θ的余弦用x表示的函数f(x);