题目内容
已知
，则f（1）+f（2）+…+f（2011）+f（2012）=（ ）A．0
B．
C．1
D．2
【答案】分析：利用和差角公式，可将函数解析式化为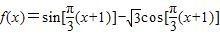
=
，结合正弦函数的图象和性质，利用分组求和法，可得答案．
解答：解：∵
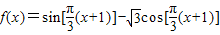=2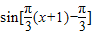
=
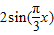
又∵y=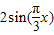
（n∈Z）的值以6为周期呈周期性变化
且在一个周期内这6项的和为0
又∵2012÷6=335…2
∴f（1）+f（2）+…+f（2011）+f（2012）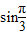
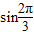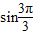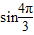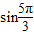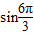=2（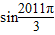
+
+
+
+
+
+…+
+
）
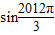=2（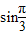
+
）
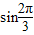=2（
+
）=2（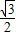
+
）=
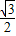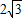
故选D
点评：本题考查的知识点是两角和与差的正弦函数，函数的值，正弦型函数的周期性，分组求和法，其中将函数的解析式化为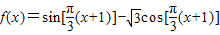
=
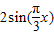是解答的关键．
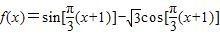=，结合正弦函数的图象和性质，利用分组求和法，可得答案．解答：解：∵
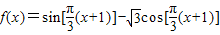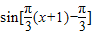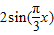
=2=又∵y=
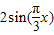（n∈Z）的值以6为周期呈周期性变化且在一个周期内这6项的和为0
又∵2012÷6=335…2
∴f（1）+f（2）+…+f（2011）+f（2012）
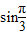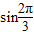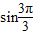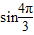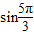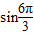=2（
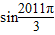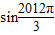++++++…++）=2（
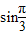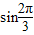+）=2（
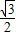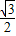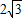
+）=2（+）=故选D
点评：本题考查的知识点是两角和与差的正弦函数，函数的值，正弦型函数的周期性，分组求和法，其中将函数的解析式化为
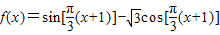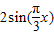=是解答的关键． 
练习册系列答案
同步轻松练习系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
，则f（1）+f（2）+f（3）+…+f（2010）= ．