题目内容
已知点A(1,0),定直线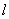 :x=-1,B为
:x=-1,B为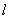 上的一个动点,过B作直线
上的一个动点,过B作直线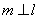 ,连接AB,作线段AB的垂直平分线n,交直线m于点M。
,连接AB,作线段AB的垂直平分线n,交直线m于点M。
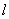 :x=-1,B为
:x=-1,B为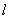 上的一个动点,过B作直线
上的一个动点,过B作直线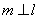 ,连接AB,作线段AB的垂直平分线n,交直线m于点M。
,连接AB,作线段AB的垂直平分线n,交直线m于点M。
(1)求点M的轨迹C的方程;
(2)过点N(4,0)作直线h与点M的轨迹C相交于不同的两点P,Q,求证:OP⊥OQ(O为坐标原点)。
(2)过点N(4,0)作直线h与点M的轨迹C相交于不同的两点P,Q,求证:OP⊥OQ(O为坐标原点)。
(1)解:由已知|MA|=|MB|,
∴M的轨迹为以A为焦点,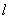 为准线的抛物线,
为准线的抛物线,
∴M的轨迹方程为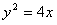 。
。
(2)证明:当h⊥x轴时,h:x=4,
由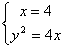 ,得
,得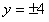 ,
,
此时,P(4,4),Q(4,-4);
当h与x轴不垂直时,设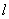 :y=k(x-4),
:y=k(x-4),
由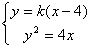 ,得
,得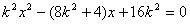 ,
,
∴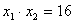 ,
,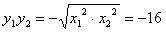 ,
,
∴ ,
,
∴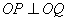 。
。
∴M的轨迹为以A为焦点,
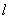 为准线的抛物线,
为准线的抛物线,∴M的轨迹方程为
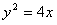 。
。(2)证明:当h⊥x轴时,h:x=4,
由
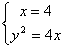 ,得
,得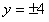 ,
,此时,P(4,4),Q(4,-4);
当h与x轴不垂直时,设
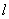 :y=k(x-4),
:y=k(x-4),由
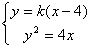 ,得
,得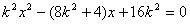 ,
,∴
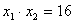 ,
,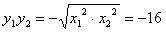 ,
,∴
 ,
,∴
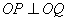 。
。
练习册系列答案
相关题目
 如图,已知点A(-1,0)与点B(1,0),C是圆x2+y2=1上的动点,连接BC并延长至D,使得|CD|=|BC|,求AC与OD的交点P的轨迹方程.
如图,已知点A(-1,0)与点B(1,0),C是圆x2+y2=1上的动点,连接BC并延长至D,使得|CD|=|BC|,求AC与OD的交点P的轨迹方程.