题目内容
已知 、
、 两盒中都有红球、白球,且球的形状、大小都相同,盒子
两盒中都有红球、白球,且球的形状、大小都相同,盒子 中有
中有 个红球与
个红球与 个白球,盒子
个白球,盒子 中有
中有 个红球与
个红球与 个白球(
个白球( ).
).
(1)分别从 、
、 中各取一个球,
中各取一个球,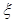 表示红球的个数;
表示红球的个数;
①请写出随机变量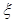 的分布列,并证明
的分布列,并证明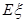 等于定值;
等于定值;
②当 为何值时,
为何值时, 取到最小值,并求出最小值.
取到最小值,并求出最小值.
(2)在盒子 中不放回地摸取3个球,事件
中不放回地摸取3个球,事件 :在第一次取到红球后,以后两次都取到白球,事件
:在第一次取到红球后,以后两次都取到白球,事件 :在第一次取到白球后,以后两次都取到红球,若概率
:在第一次取到白球后,以后两次都取到红球,若概率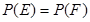 ,求
,求 的值.
的值.
 、
、 两盒中都有红球、白球,且球的形状、大小都相同,盒子
两盒中都有红球、白球,且球的形状、大小都相同,盒子 中有
中有 个红球与
个红球与 个白球,盒子
个白球,盒子 中有
中有 个红球与
个红球与 个白球(
个白球( ).
).(1)分别从
 、
、 中各取一个球,
中各取一个球,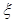 表示红球的个数;
表示红球的个数;①请写出随机变量
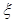 的分布列,并证明
的分布列,并证明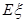 等于定值;
等于定值;②当
 为何值时,
为何值时, 取到最小值,并求出最小值.
取到最小值,并求出最小值.(2)在盒子
 中不放回地摸取3个球,事件
中不放回地摸取3个球,事件 :在第一次取到红球后,以后两次都取到白球,事件
:在第一次取到红球后,以后两次都取到白球,事件 :在第一次取到白球后,以后两次都取到红球,若概率
:在第一次取到白球后,以后两次都取到红球,若概率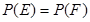 ,求
,求 的值.
的值.(1)①见解析 ②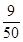 (2)5
(2)5
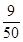 (2)5
(2)5试题分析:(1)①先确定
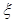 的取值,再分别求出
的取值,再分别求出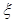 等于0、1、2时的概率,然后即可列表,确定
等于0、1、2时的概率,然后即可列表,确定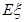 为定值②将值带入公式求解即可.(2)先求出事件E和F的概率表达式为
为定值②将值带入公式求解即可.(2)先求出事件E和F的概率表达式为 ;
;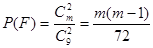 ,然后根据两式相等,即可求出m的值.
,然后根据两式相等,即可求出m的值.试题解析:(1)①
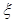 的可能取值为0,1,2 1分
的可能取值为0,1,2 1分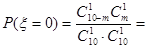
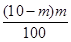
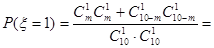
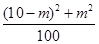
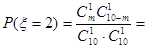
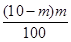 4分
4分∴
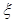 分布列为:
分布列为: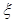 | 0 | 1 | 2 |
 | 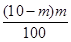 | 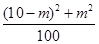 | 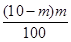 |
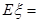
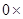
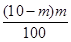
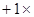
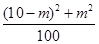
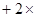
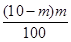
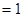 为定值 6分
为定值 6分②
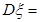
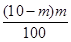
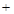
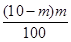
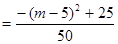 7分
7分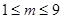 ,
, ,当
,当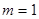 或
或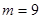 时,
时, 最小,最小值为
最小,最小值为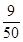 . 9分
. 9分(2)
 ,
,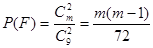 11分
11分∵
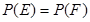 ∴
∴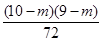
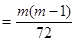 ∴
∴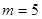 14分
14分
练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
 .
.

 ,其中
,其中 )
)






