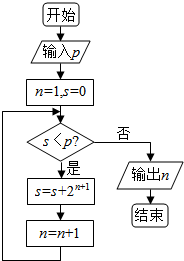
题目内容
14.求证.cosα+cos3α=2cos2αcosα.分析 根据题意,由于α=2α-α,3α=α+2α,则左式可以变形为cos(2α-α)+cos(α+2α),利用余弦的和差公式变形可得左式=2cos2αcosα,即可得证明.
解答 解:根据题意,由于α=2α-α,3α=α+2α,
则左式=cosα+cos3α=cos(2α-α)+cos(α+2α)
=(cosαcos2α+sinαsin2α)+(cosαcos2α-sinαsin2α)
=2cos2αcosα=右式;
即原等式得证.
点评 本题考查余弦的和差公式的运用,解题的关键是角的转化,即α=2α-α,3α=α+2α.

练习册系列答案
相关题目
9.函数y=x2+4x在x=-1处的导数是( )
| A. | -3 | B. | 2 | C. | -6 | D. | 3 |
11.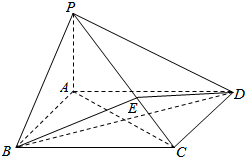 如图所示,在四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,点E在线段PC上,PC⊥平面BDE.
如图所示,在四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,点E在线段PC上,PC⊥平面BDE.
(I)证明:BD⊥平面PAC;
(Ⅱ)若PA=1,AD=2,求点B到平面PCD的距离.
 如图所示,在四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,点E在线段PC上,PC⊥平面BDE.
如图所示,在四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,点E在线段PC上,PC⊥平面BDE.(I)证明:BD⊥平面PAC;
(Ⅱ)若PA=1,AD=2,求点B到平面PCD的距离.
8.若点P是抛物线x2=4y上一动点,则点P到直线x-2y-3=0和x轴的距离之和的最小值是( )
| A. | $\sqrt{3}$ | B. | $\sqrt{5}$ | C. | 2 | D. | $\sqrt{5}-1$ |
9.从某企业生产的某种产品中抽取100件,测量这些产品的一项质量指标值,由测量表得如下频数分布表:
(Ⅰ)在答题卡上作出这些数据的频率分布直方图:
(Ⅱ)估计这种产品质量指标值的众数、中位数及平均数(同一组中的数据用该组区间的中点值作代表);
(Ⅲ)根据以上抽样调查数据,能否认为该企业生产的这种产品符合“质量指标值不低于95的产品至少要占全部产品的80%”的规定?
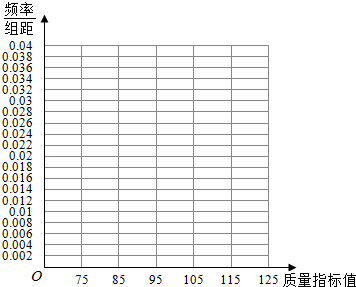
| 质量指标值分组 | [75,85) | [85,95) | [95,105) | [105,115) | [115,125) |
| 频数 | 6 | 26 | 38 | 22 | 8 |
(Ⅱ)估计这种产品质量指标值的众数、中位数及平均数(同一组中的数据用该组区间的中点值作代表);
(Ⅲ)根据以上抽样调查数据,能否认为该企业生产的这种产品符合“质量指标值不低于95的产品至少要占全部产品的80%”的规定?