题目内容
已知f(x)是定义在R上的函数,给出下列两个命题:p:若f(x1)=f(x2),(x1≠x2),则x1+x2=4.
q:若x1,x2∈(-∞,2](x1≠x2),则

则使命题“p且q”为真命题的函数f(x)可以是 .
【答案】分析:命题“p且q”为真命题,命题p,q均为真命题.p为真命题说明函数f(x)图象关于直线x=2对称.q为真命题,可以推出f(x)在(-∞,2]上单调递增.可以想到二次函数.
解答:解:命题“p且q”为真命题,命题p,q均为真命题.
p:若f(x1)=f(x2),(x1≠x2),则x1+x2=4.说明函数f(x)图象关于直线x=2对称.
若x1,x2∈(-∞,2](x1≠x2),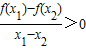 ,说明当x1>x2时,f(x1)>f(x2),所以f(x)在(-∞,2]上单调递增.
,说明当x1>x2时,f(x1)>f(x2),所以f(x)在(-∞,2]上单调递增.
根据以上性质,f(x)可以是,f(x)=-(x-2)2
故答案为:f(x)=-(x-2)2.
点评:本题以复合命题真假出发,考查了初等函数的性质.考查转化、数形结合的思想.
解答:解:命题“p且q”为真命题,命题p,q均为真命题.
p:若f(x1)=f(x2),(x1≠x2),则x1+x2=4.说明函数f(x)图象关于直线x=2对称.
若x1,x2∈(-∞,2](x1≠x2),
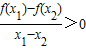 ,说明当x1>x2时,f(x1)>f(x2),所以f(x)在(-∞,2]上单调递增.
,说明当x1>x2时,f(x1)>f(x2),所以f(x)在(-∞,2]上单调递增.根据以上性质,f(x)可以是,f(x)=-(x-2)2
故答案为:f(x)=-(x-2)2.
点评:本题以复合命题真假出发,考查了初等函数的性质.考查转化、数形结合的思想.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目