题目内容
【题目】如图,在直三棱柱ABC﹣A1B1C1中,AB⊥AC,AB=BB1=1,B1C=2. 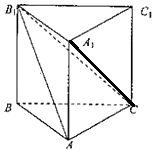
(1)求证:平面B1AC⊥平面ABB1A1;
(2)求直线A1C与平面B1AC所成角的正弦值.
【答案】
(1)证明:由直三棱柱性质,B1B⊥平面ABC;
∴B1B⊥AC;
又AB⊥AC,B1B∩BA=B;
∴AC⊥平面ABB1A1,AC平面B1AC;
∴平面B1AC⊥平面ABB1A1;
(2)解:如图,连接A1B交AB1于M,连接CM;
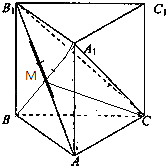
∵AB=BB1;
∴A1B1=AA1;
∴A1M⊥AB1;
∵平面B1AC⊥平面ABB1A,且平面B1AC∩平面ABB1A1=B1A;
∴A1M⊥平面B1AC;
∴∠A1CM为直线A1C与平面B1AC所成的角;
∵AB=BB1=1,B1C=2;
∴BC= ![]() ,AC=
,AC= ![]() ;
;
∴ ![]() ;
;
∴ ![]() ;
;
∴直线A1C与平面B1AC所成角的正弦值为 ![]() .
.
【解析】(1)根据直三棱柱的定义便可得到AC⊥B1B,再根据条件AC⊥AB便可得出AC⊥平面ABB1A1 , 从而由面面垂直的判定定理即可得出平面B1AC⊥平面ABB1A1;(2)可连接A1B,设交AB1于M,可得到A1M⊥AB1 , 从而由面面垂直的性质定理得到A1M⊥平面B1AC,这样∠A1CM便是直线A1C与平面B1AC所成的角,根据条件便可求出A1M和A1C的长,由 ![]() 即可得出直线A1C与平面B1AC所成角的正弦值.
即可得出直线A1C与平面B1AC所成角的正弦值.
【考点精析】通过灵活运用平面与平面垂直的判定和空间角的异面直线所成的角,掌握一个平面过另一个平面的垂线,则这两个平面垂直;已知![]() 为两异面直线,A,C与B,D分别是
为两异面直线,A,C与B,D分别是![]() 上的任意两点,
上的任意两点,![]() 所成的角为
所成的角为![]() ,则
,则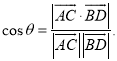 即可以解答此题.
即可以解答此题.

【题目】某城市随机抽取一年内100 天的空气质量指数(AQI)的监测数据,结果统计如表:
API | [0,50] | (50,100] | (100,150] | (150,200] | (200,300] | >300 |
空气质量 | 优 | 良 | 轻度污染 | 轻度污染 | 中度污染 | 重度污染 |
天数 | 6 | 14 | 18 | 27 | 20 | 15 |
(1)若本次抽取的样本数据有30 天是在供暖季,其中有8 天为严重污染.根据提
供的统计数据,完成下面的2×2 列联表,并判断是否有95%的把握认为“该城市本年的
空气严重污染与供暖有关”?
非重度污染 | 严重污染 | 合计 | |
供暖季 | |||
非供暖季 | |||
合计 | 100 |
(2)已知某企业每天的经济损失y(单位:元)与空气质量指数x 的关系式为y=  试估计该企业一个月(按30 天计算)的经济损失的数学期望.
试估计该企业一个月(按30 天计算)的经济损失的数学期望.
参考公式:K2= ![]()
P(K2≥k) | 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
k | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |