题目内容
【题目】已知等差数列{an}的前n项和为Sn ， 且a3=3，S7=28，在等比数列{bn}中，b3=4，b4=8．
（1）求an及bn；
（2）设数列{anbn}的前n项和为Tn ， 求Tn ．
【答案】
（1）解：设{an}的公差为d，则由题a3=3，S7=28，
有 
，
∴an=n．
∵在等比数列{bn}中，b3=4，b4=8，
∴{bn}的公比为 
，∴ 
，
即 
．
（2）由（1）知an=n， ，∴ 
．
∴ 
，
，
∴ 
，
即 
．
【解析】（1）根据等差数列，等比数列的通项公式，前n项和的公式可得结果，（2）根据通项公式表示出
，再用错位相减得出Tn.
【考点精析】解答此题的关键在于理解数列的前n项和的相关知识，掌握数列{an}的前n项和sn与通项an的关系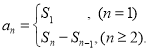
．
练习册系列答案
相关题目
【题目】为了解某社区居民购买水果和牛奶的年支出费用与购买食品的年支出费用的关系，随机调查了该社区5户家庭，得到如下统计数据表：
购买食品的年支出费用x（万元） | 2.09 | 2.15 | 2.50 | 2.84 | 2.92 |
购买水果和牛奶的年支出费用y（万元） | 1.25 | 1.30 | 1.50 | 1.70 | 1.75 |
根据上表可得回归直线方程 
，其中 
，据此估计，该社区一户购买食品的年支出费用为3.00万元的家庭购买水果和牛奶的年支出费用约为（ ）
A.1.79万元
B.2.55万元
C.1.91万元
D.1.94万元
