题目内容
7.用lgx,lgy,lgz,lg(x+y),lg(x-y)表示下列各式(其中x>y>0,z>0):(1)lg(xyz);
(2)lg(xy-2z-1);
(3)lg(x2y2z-3);
(4)lg$\frac{\sqrt{x}}{{y}^{3}z}$;
(5)lg$\frac{xy}{({x}^{2}-{y}^{2})}$;
(6)lg($\frac{x+y}{x-y}$•y);
(7)lg[$\frac{y}{x(x-y)}$]3.
分析 直接利用对数的运算性质逐一化简各式得答案.
解答 解:(1)lg(xyz)=lgx+lgy+lgz;
(2)lg(xy-2z-1)=lgx-2lgy-lgz;
(3)lg(x2y2z-3)=2lgx+2lgy-3lgz;
(4)lg$\frac{\sqrt{x}}{{y}^{3}z}$=$\frac{1}{2}$lgx-3lgy-lgz;
(5)lg$\frac{xy}{({x}^{2}-{y}^{2})}$=lgx+lgy-lg(x+y)-lg(x-y);
(6)lg($\frac{x+y}{x-y}$•y)=lg(x+y)-lg(x-y)+lgy;
(7)lg[$\frac{y}{x(x-y)}$]3=3lgy-3lgx-3lg(x-y).
点评 本题考查对数的运算性质,是基础的计算题.

练习册系列答案
相关题目
18.设函数f(x)=ax3+bx+2,若f(2)=8,则f(-2)=( )
| A. | -8 | B. | -6 | C. | -4 | D. | -2 |
2.菱形的对角线相等,正方形是菱形,所以正方形的对角线相等.在以上三段论的推理中( )
| A. | 大前提错误 | B. | 小前提错误 | C. | 推理形式错误 | D. | 结论错误 |
9.七个同学参加三个兴趣小组,每人只能参加一个兴趣小组,每个兴趣小组至少两个同学,则不同的参加方法有( )
| A. | 630种 | B. | 210种 | C. | 420种 | D. | 1890种 |
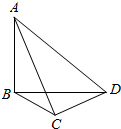 若电视塔AB的高度为30米,且在D,C两点的仰视角分别为45度和60度,且∠DBC=30°,则C,D两点间的距离是多少米.
若电视塔AB的高度为30米,且在D,C两点的仰视角分别为45度和60度,且∠DBC=30°,则C,D两点间的距离是多少米.