题目内容
6.某学生参加3门课程的考试,假设该学生第一门课程取得优秀成绩的概率为$\frac{3}{4}$,第二门、第三门课程取得优秀成绩的概率分别为p,q(p>q),且不同课程是否取得优秀成绩相可独立,记X为该生取得优秀成绩的课程数,已知p(X=0)=P(X=3)=$\frac{3}{32}$.(1)求p、q的值;
(2)求X的数学期望E(X).
分析 (1)用A表示“该生第一门课程取得优秀成绩”,用B表示“该生第二门课程取得优秀成绩”,用C表示“该生第三门课程取得优秀成绩”,由题意得P($\overline{A}\overline{B}\overline{C}$)=(1-$\frac{3}{4}$)(1-p)(1-q)=$\frac{3}{32}$,P(ABC)=$\frac{3}{4}$pq=$\frac{3}{32}$,由此能求出p,q.
(2)由题设知X的可能取值为0,1,2,3,分别求出其概率,由此能够求出数学期望E(X).
解答 解:(1)用A表示“该生第一门课程取得优秀成绩”,用B表示“该生第二门课程取得优秀成绩”,用C表示“该生第三门课程取得优秀成绩”,
由题意得P(A)=$\frac{3}{4}$,P(B)=p,P(C)=q,p>q,
P($\overline{A}\overline{B}\overline{C}$)=(1-$\frac{3}{4}$)(1-p)(1-q)=$\frac{3}{32}$,
P(ABC)=$\frac{3}{4}$pq=$\frac{3}{32}$,
解得p=$\frac{1}{2}$,q=$\frac{1}{4}$.
(2)由题设知X的可能取值为0,1,2,3,
P(X=0)=$\frac{3}{32}$,
P(X=1)=$\frac{3}{4}$×(1-$\frac{1}{2}$)×(1-$\frac{1}{4}$)+(1-$\frac{3}{4}$)×$\frac{1}{2}$×(1-$\frac{1}{4}$)+(1-$\frac{3}{4}$)×(1-$\frac{1}{2}$)×$\frac{1}{4}$=$\frac{13}{32}$,
P(X=2)=$\frac{3}{4}$×$\frac{1}{2}$×(1-$\frac{1}{4}$)+$\frac{3}{4}$×(1-$\frac{1}{2}$)×$\frac{1}{4}$+(1-$\frac{3}{4}$)×$\frac{1}{2}$×$\frac{1}{4}$=$\frac{13}{32}$,
P(X=3)=$\frac{3}{32}$,
∴E(X)=0×$\frac{3}{32}$+1×$\frac{13}{32}$+2×$\frac{13}{32}$+3×$\frac{3}{32}$=1.5.
点评 本题考查离散随机变量的概率分布列和数学期望,是历年高考的必考题型之一.解题时要认真审题,注意排列组合知识和概率知识的灵活运用.

| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
①方程f(x)=0至少有一个实数根;
②方程f(x)=0至多有两个实数根;
③函数f(x)的图象关于点(0,c)对称;
④当b≥0时,f(x)在R上是增函数.
其中正确的结论是( )
| A. | ①② | B. | ②③ | C. | ③④ | D. | ①③④ |
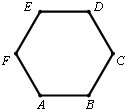
| A. | $\overrightarrow{AE}$•$\overrightarrow{FC}$=0 | B. | $\overrightarrow{AE}$•$\overrightarrow{DF}$>0 | C. | $\overrightarrow{FC}$=$\overrightarrow{FD}$+$\overrightarrow{FB}$ | D. | $\overrightarrow{FD}$•$\overrightarrow{FB}$<0 |

| A. | $\sqrt{3}$ | B. | 2 | C. | 2$\sqrt{3}$ | D. | 6 |
 某地区有800名学员参加交通法规考试,考试成绩的频率分布直方图如图所示.其中成绩分组区间是:[75,80),[80,85),[85,90),[90,95),[95,100].规定90分及其以上为合格.
某地区有800名学员参加交通法规考试,考试成绩的频率分布直方图如图所示.其中成绩分组区间是:[75,80),[80,85),[85,90),[90,95),[95,100].规定90分及其以上为合格.