题目内容
(09年海淀区二模文)(14分)
数列![]()
(1)当![]() 时,求实数
时,求实数![]() 及a3;
及a3;
(2)是否存在实数![]() ,使得数列{
,使得数列{![]() }为等差数列?若存在,求数列{
}为等差数列?若存在,求数列{![]() }的通项公式,若不存在,说明理由.
}的通项公式,若不存在,说明理由.
解析:(I)![]()
![]()
![]() ………………………………3分
………………………………3分
(II)![]()
![]()
若数列![]() 为等差数列,则
为等差数列,则![]() ………………6分
………………6分
![]() 方程没有实根, ………………7分
方程没有实根, ………………7分
故不存在实数![]() ,使得数列
,使得数列![]() 为等差数列. …………………8分
为等差数列. …………………8分
(III)![]()
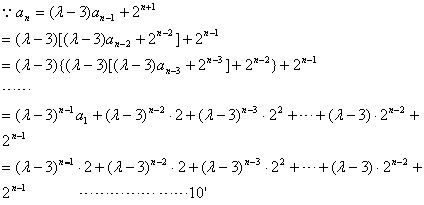
若![]() =3,则
=3,则![]() ……………………10分
……………………10分
若![]() 3,则数列
3,则数列![]()
![]() 从第二项起,是一个首项为2
从第二项起,是一个首项为2![]() ,公比为
,公比为![]() 的等比数列.
的等比数列.
如果![]() =1,即
=1,即![]() =5时,
=5时,
![]()
如果![]()
![]() 1,即
1,即![]()
![]() 5时,
5时,
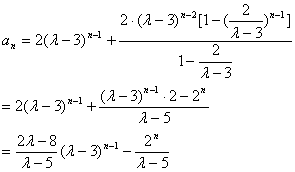
![]()
当![]() =3时,
=3时,![]() ,与前面的计算结果相符,
,与前面的计算结果相符,
故数列![]() 的通项公式为
的通项公式为
 …………………………14分
…………………………14分

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目