题目内容
2.已知$|{\overrightarrow a}|=2,|{\overrightarrow b}$$|=4,\overrightarrow a与\overrightarrow b$的夹角为$\frac{π}{3}$,以$\overrightarrow a,\overrightarrow b$为邻边作平行四边形,则此平行四边形的两条对角线中较长的一条的长度为$2\sqrt{7}$.分析 根据向量加法的平行四边形法则便可知道较长的一条对角线长度应是$|\overrightarrow{a}+\overrightarrow{b}|$,根据条件$(\overrightarrow{a}+\overrightarrow{b})^{2}$能求出,从而得出|$\overrightarrow{a}+\overrightarrow{b}$|.
解答 解:平行四边形的两条对角线中较长的一条的长度为|$\overrightarrow{a}+\overrightarrow{b}$|=$\sqrt{(\overrightarrow{a}+\overrightarrow{b})^{2}}$=$\sqrt{4+8+16}$=$2\sqrt{7}$.
故答案为:2$\sqrt{7}$.
点评 考查向量加法的平行四边形法则,向量$\overrightarrow{a}+\overrightarrow{b}$长度的求法:$|\overrightarrow{a}+\overrightarrow{b}|=\sqrt{(\overrightarrow{a}+\overrightarrow{b})^{2}}$,以及数量积的计算公式.

练习册系列答案
相关题目
14.已知{an}为等比数列,且a3•a9=2a52,a1=1,则a3=( )
| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $\sqrt{2}$ | D. | 2 |
11.若x,y满足约束条件$\left\{\begin{array}{l}x+y≥1\\ x-y≥-1\\ 2x-y≤2\end{array}\right.$,目标函数z=ax+2y仅在点(1,0)处取得最小值,则a的取值范围是( )
| A. | (-1,2 ) | B. | (-4,2 ) | C. | (-4,0] | D. | (-2,4) |
12.如图的程序框图表示求式子1×3×7×15×31×63的值,则判断框内可以填的条件为( )
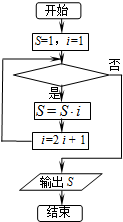

| A. | i≤31? | B. | i≤63? | C. | i≥63? | D. | i≤127? |