题目内容
已知函数 (
( 为常数,
为常数, 是自然对数的底数),曲线
是自然对数的底数),曲线 在点
在点 处的切线与
处的切线与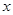 轴平行.
轴平行.
(Ⅰ)求 的值;
的值;
(Ⅱ)求 的单调区间;
的单调区间;
(Ⅲ)设 ,其中
,其中 为
为 的导函数.证明:对任意
的导函数.证明:对任意 .
.
【答案】
:(Ⅰ) ;
;
(Ⅱ) 的单调增为
的单调增为 单调减区为
单调减区为 .
.
(Ⅲ)见解析
【解析】:函数 的定义域为
的定义域为
(Ⅰ) ,
,
由题意可知 所以
所以
(Ⅱ) ,
,
当 时,
时, ,所以
,所以 ,
,
当 时,
时, ,所以
,所以 ,
,
即 的单调增为
的单调增为 单调减区为
单调减区为
(Ⅲ) .
.
显然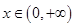 时,
时, ,
,
所以
要证 ,只须证
,只须证 ,即
,即 .
.
下面 求 的最小值.
的最小值.

当 时
时 当
当 时
时
所以 的最小值为
的最小值为

即 .
.
命题得证.
【考点定位】本题考函数的单调性、导数及其应用、切线等知识,并对分类讨论思想、逻辑推理论证进行考查。第三问通过分析法使问题得证,并体现构造思想,是近几年来少有的考查方式

练习册系列答案
相关题目
 (
( 为常数)是奇函数,则实数
为常数)是奇函数,则实数 为( )
为( ) C.
3
D.
C.
3
D. 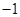
 (
( 为常数,
为常数,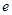 是自然对数的底数)是实数集
是自然对数的底数)是实数集 上的奇函数.
上的奇函数. 的零点的个数.
的零点的个数.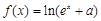 (
( 为常数)是实数集
为常数)是实数集 上的奇函数,函数
上的奇函数,函数 是区间[-1,1]上的减函数.
是区间[-1,1]上的减函数. 在
在 及
及 所在的取值范围上恒成立,求
所在的取值范围上恒成立,求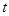 的取值范围;
的取值范围; 的方程
的方程 的根的个数.
的根的个数.