题目内容
已知A,B,C三点的坐标分别是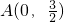 ,B(0,3),C(cosθ,sinθ),其中
,B(0,3),C(cosθ,sinθ),其中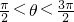 ,且
,且 .
.
(1)求角θ的值;
(2)当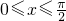 时,求函数f(x)=2sin(2x+θ)的最大值和最小值.
时,求函数f(x)=2sin(2x+θ)的最大值和最小值.
解:(1)∵A,B,C三点的坐标分别是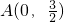 ,B(0,3),C(cosθ,sinθ),
,B(0,3),C(cosθ,sinθ),
∴ =(cosθ-3,sinθ),
=(cosθ-3,sinθ), =(cosθ,sinθ-3)…(2分)
=(cosθ,sinθ-3)…(2分)
∵ ,∴
,∴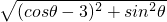 =
=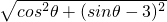
化简得:sinθ=cosθ …(5分)
∵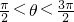 ,∴θ=
,∴θ= …(7分)
…(7分)
(2)当0≤x≤ 时,
时,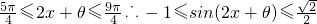 …(10分)
…(10分)
∴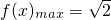 ,f(x)min=-2…(12分)
,f(x)min=-2…(12分)
分析:(1)确定 、
、 的坐标,利用
的坐标,利用 ,建立方程,即可求角θ的值;
,建立方程,即可求角θ的值;
(2)当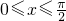 时,可得2x+θ的范围,利用正弦函数的性质,即可求函数f(x)=2sin(2x+θ)的最大值和最小值.
时,可得2x+θ的范围,利用正弦函数的性质,即可求函数f(x)=2sin(2x+θ)的最大值和最小值.
点评:本题考查向量知识的运用,考查正弦函数的性质,考查学生的计算能力,属于中档题.
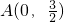 ,B(0,3),C(cosθ,sinθ),
,B(0,3),C(cosθ,sinθ),∴
 =(cosθ-3,sinθ),
=(cosθ-3,sinθ), =(cosθ,sinθ-3)…(2分)
=(cosθ,sinθ-3)…(2分)∵
 ,∴
,∴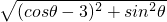 =
=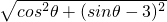
化简得:sinθ=cosθ …(5分)
∵
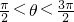 ,∴θ=
,∴θ= …(7分)
…(7分)(2)当0≤x≤
 时,
时,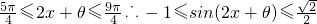 …(10分)
…(10分)∴
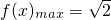 ,f(x)min=-2…(12分)
,f(x)min=-2…(12分)分析:(1)确定
 、
、 的坐标,利用
的坐标,利用 ,建立方程,即可求角θ的值;
,建立方程,即可求角θ的值;(2)当
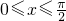 时,可得2x+θ的范围,利用正弦函数的性质,即可求函数f(x)=2sin(2x+θ)的最大值和最小值.
时,可得2x+θ的范围,利用正弦函数的性质,即可求函数f(x)=2sin(2x+θ)的最大值和最小值.点评:本题考查向量知识的运用,考查正弦函数的性质,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目