题目内容
已知函数f(x)=log2
,g(x)=2ax+1-a,又h(x)=f(x)+g(x)
(1)求函数f(x)的定义域;(2)试讨论h(x)的奇偶性;
(3)若关于x的方程f(x)=log2g(x)有两个不等实数根,求a的取值范围.
| x-1 | x+1 |
(1)求函数f(x)的定义域;(2)试讨论h(x)的奇偶性;
(3)若关于x的方程f(x)=log2g(x)有两个不等实数根,求a的取值范围.
分析:(1)根据让函数解析式有意义的原则,结合对数函数真为大于0,构造关于x的不等式,解不等式可得答案.
(2)根据已知可分a=1和a≠1时两种情况,分别讨论h(-x)+h(x)与h(-x)-h(x)与0的关系,进而根据函数奇偶性的定义可得答案
(3)方程f(x)=log2g(x)有两个不等实数根,即
=2ax+1-a在(-∞,-1)∪(1,+∞)上有两个不等的根,即a=-
在(-∞,-1)∪(1,+∞)上有两个不等的根,借助函图象易分析出a的取值范围.
(2)根据已知可分a=1和a≠1时两种情况,分别讨论h(-x)+h(x)与h(-x)-h(x)与0的关系,进而根据函数奇偶性的定义可得答案
(3)方程f(x)=log2g(x)有两个不等实数根,即
| x-1 |
| x+1 |
| 2 |
| 2x2+x+1 |
解答:解:(1)要使函数f(x)=log2
的解析式有意义
则
>0
解得x<-1,或x>1
即函数f(x)=log2
的定义域为(-∞,-1)∪(1,+∞),
(2)当a=1时,h(x)=f(x)+g(x)=log2
+2x,
∵h(-x)+h(x)=0,
∴h(x)为奇函数;
当a≠1时,h(x)=f(x)+g(x)=log2
+2ax+1-a,
∵h(-2)+h(2)=2-2a≠0
故h(x)为非奇函数
令h(-3)-h(3)=12a-2=0,则a=
此时,h(-2)-h(2)≠0
故h(x)为非偶函数
综上h(x)既不是奇函数又不是偶函数;
(3)f(x)=log2g(x)有两个零点等价于
=2ax+1-a在(-∞,-1)∪(1,+∞)上有两个不等的根;
即a=-
在(-∞,-1)∪(1,+∞)上有两个不等的根;
由y=-
在(-∞,-1)∪(1,+∞)上的图象可得
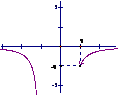
a的取值范围-1<a<0
| x-1 |
| x+1 |
则
| x-1 |
| x+1 |
解得x<-1,或x>1
即函数f(x)=log2
| x-1 |
| x+1 |
(2)当a=1时,h(x)=f(x)+g(x)=log2
| x-1 |
| x+1 |
∵h(-x)+h(x)=0,
∴h(x)为奇函数;
当a≠1时,h(x)=f(x)+g(x)=log2
| x-1 |
| x+1 |
∵h(-2)+h(2)=2-2a≠0
故h(x)为非奇函数
令h(-3)-h(3)=12a-2=0,则a=
| 1 |
| 6 |
此时,h(-2)-h(2)≠0
故h(x)为非偶函数
综上h(x)既不是奇函数又不是偶函数;
(3)f(x)=log2g(x)有两个零点等价于
| x-1 |
| x+1 |
即a=-
| 2 |
| 2x2+x-1 |
由y=-
| 2 |
| 2x2+x-1 |

a的取值范围-1<a<0
点评:本题考查的知识点是函数的零点与方程根的关键,函数的定义域,函数的奇偶性,其中(3)中将方程的根转化为函数图象与y=a交点的个数,并用图象法进行解答是转化思想是解非基本方程是的重要应用.

练习册系列答案
相关题目