题目内容
过点A(4,1)且在两坐标轴上的截距相等的直线方程是( )
| A.x+y=5 | B.x-y=5 |
| C.x+y=5或x-4y=0 | D.x-y=5或x+4y=0 |
C
解析试题分析: 设过点A(4,1)的直线方程为y-1=k(x-4)(k≠0),令x=0,得y=1-4k;令y=0,得x=4-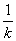 .由已知得1-4k=4-
.由已知得1-4k=4-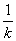 ,∴k=-1或k=
,∴k=-1或k=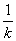 ,∴所求直线方程为x+y-5=0或x-4y=0。
,∴所求直线方程为x+y-5=0或x-4y=0。
考点:直线方程的求法。
点评:此题若用截距式求直线方程,应讨论截距均为0的情况,否则易错。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
两条直线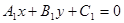 与
与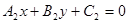 垂直的充分不必要条件是( )
垂直的充分不必要条件是( )
A.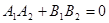 | B.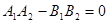 |
C.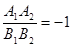 | D.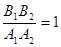 |
若三点 ,
,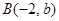 ,
, 在同一直线上,则实数
在同一直线上,则实数 等于
等于
| A.2 | B.3 | C.9 | D. |
过点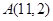 作圆
作圆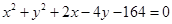 的弦,其中弦长为整数的共有 ( )
的弦,其中弦长为整数的共有 ( )
| A.16条 | B.17条 | C.32条 | D.34条 |
两条平行线l1:3x-4y-1=0与l2:6x-8y-7=0间的距离为( )
A.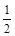 | B.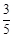 | C.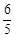 | D.1 |
直线 :
: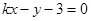 和
和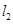 :
: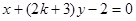 互相垂直,则
互相垂直,则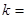 ( )
( )
| A.-2 | B.-3 | C.-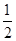 或-1 或-1 | D.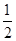 或1 或1 |
已知直线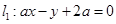 ,
,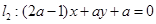 互相垂直,则
互相垂直,则 的值是( )
的值是( )
A. | B.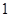 | C. 或 或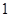 | D. 或 或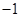 |
在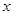 轴上的截距为2且倾斜角为135°的直线方程为 ( )
轴上的截距为2且倾斜角为135°的直线方程为 ( )
| A.y=-x+2 | B.y=-x-2 | C.y=x+2 | D.y=x-2 |
点(-1,2)关于直线y ="x" -1的对称点的坐标是
| A.(3,2) | B.(-3,-2) |
| C.(-3,2) | D.(3,-2) |