题目内容
在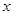
轴上的截距为2且倾斜角为135°的直线方程为 （ ）
| A．ｙ＝－ｘ＋２ | B．ｙ＝－ｘ－２ | C．ｙ＝ｘ＋２ | D．ｙ＝ｘ－２ |
A
解析试题分析：倾斜角为135°，所以斜率为-1，由直线方程的斜截式可知直线方程为
ｙ＝－ｘ＋２.
考点：本小题主要考查由斜截式求直线方程.
点评：直线方程的五种形式要牢固掌握，灵活应用.
练习册系列答案
金版课堂课时训练系列答案
单元全能练考卷系列答案
新黄冈兵法密卷系列答案
相关题目
直线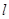
的斜率是3，且过点A（1,-2）,则直线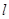的方程是（ ）
A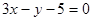． | B． |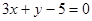
C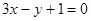． | D． |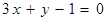
过点A(4，1)且在两坐标轴上的截距相等的直线方程是( )
| A．x+y=5 | B．x-y=5 |
| C．x+y=5或x-4y=0 | D．x-y=5或x+4y=0 |
如果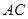
＜0，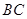
＜0，那么直线
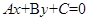不通过( )
| A．第一象限 | B．第二象限 | C．第三象限 | D．第四象限 |
（文科） 两条直线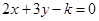
和
的交点在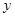
轴上，那么
的值是 （ ）
| A．－24 | B．6 | C．±6 | D．24 |
经过点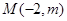
、
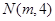的直线的斜率等于1，则
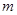的值为
| A．1 | B．4 | C．1或3 | D．1或4 |
4．已知过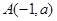
、
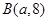两点的直线与直线
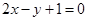平行，则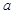
的值为（ ）
A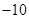． | B． | C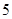． | D． |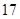
直线的斜率为
，其倾斜角的大小是（ ）
| A．30º | B． 45º | C．90º | D．135º |
已知直线
不经过第一象限，且
，则直线
的倾斜角的取值范围是（ ）
A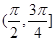． | B． | C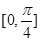． | D． |