题目内容
设曲C的参数方程为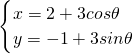
（θ为参数），直线l的方程为x-3y+2=0，则曲线C上到直线l距离为
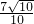的点的个数为________．
2
分析：将圆C的方程化为一般方程，可以计算圆心到直线l距离为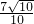，结合圆的半径为3，即可得出结论．
解答：化曲线C的参数方程为普通方程：（x-2）2+（y+1）2=9，
∵圆心（2，-1）到直线x-3y+2=0的距离
，
∴直线和圆相交，且过圆心和l平行的直线和圆的2个交点符合要求，
又∵
，
∴在直线l的另外一侧没有圆上的点符合要求，
故答案为：2．
点评：本题以圆的参数方程为载体，考查点线距离公式的运用，解题的关键是判断直线与圆的位置关系，利用圆的图形，从而得解
分析：将圆C的方程化为一般方程，可以计算圆心到直线l距离为
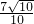，结合圆的半径为3，即可得出结论．解答：化曲线C的参数方程为普通方程：（x-2）2+（y+1）2=9，
∵圆心（2，-1）到直线x-3y+2=0的距离
，∴直线和圆相交，且过圆心和l平行的直线和圆的2个交点符合要求，
又∵
，∴在直线l的另外一侧没有圆上的点符合要求，
故答案为：2．
点评：本题以圆的参数方程为载体，考查点线距离公式的运用，解题的关键是判断直线与圆的位置关系，利用圆的图形，从而得解
练习册系列答案
培优口算题卡系列答案
开心口算题卡系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
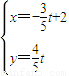，（t为参数）设直线L与x轴的交点M，N是曲线C上一动点，求|MN|的最大值 ．