题目内容
已知曲C的极坐标方程ρ=2sinθ,设直线L的参数方程
,(t为参数)设直线L与x轴的交点M,N是曲线C上一动点,求|MN|的最大值
+1
+1.
|
| 5 |
| 5 |
分析:首先将曲线C化成普通方程,得出它是以P(0,1)为圆心半径为1的圆,然后将直线L化成普通方程,得出它与x轴的交点M的坐标,最后用两个点之间的距离公式得出PM的距离,从而得出曲C上一动点N到M的最大距离.
解答:解:∵曲线C的极坐标方程ρ=2sinθ,化成普通方程:
x2+y2-2y=0,即x2+(y-1)2=1
∴曲线C表示以点P(0,1)为圆心,半径为1的圆
∵直L的参数方程是:
∴直L的普通方程是:4x+3y-8=0
∴可得L与x轴的交点M坐标为(2,0)
∴PM=
=
由此可得曲C上一动点N到M的最大距离等于
+1
故答案为:
+1
x2+y2-2y=0,即x2+(y-1)2=1
∴曲线C表示以点P(0,1)为圆心,半径为1的圆
∵直L的参数方程是:
|
∴直L的普通方程是:4x+3y-8=0
∴可得L与x轴的交点M坐标为(2,0)
∴PM=
| (2-0) 2+(0-1) 2 |
| 5 |
由此可得曲C上一动点N到M的最大距离等于
| 5 |
故答案为:
| 5 |
点评:本题考查了简单的曲线的极坐标方程和参数方程化为普通方程、以及圆上动点到圆外一个定点的距离最值的知识点,属于中档题.

练习册系列答案
相关题目
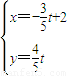 ,(t为参数)设直线L与x轴的交点M,N是曲线C上一动点,求|MN|的最大值 .
,(t为参数)设直线L与x轴的交点M,N是曲线C上一动点,求|MN|的最大值 .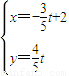 ,(t为参数)设直线L与x轴的交点M,N是曲线C上一动点,求|MN|的最大值 .
,(t为参数)设直线L与x轴的交点M,N是曲线C上一动点,求|MN|的最大值 .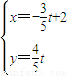 ,(t为参数)设直线L与x轴的交点M,N是曲线C上一动点,求|MN|的最大值 .
,(t为参数)设直线L与x轴的交点M,N是曲线C上一动点,求|MN|的最大值 .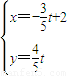 ,(t为参数)设直线L与x轴的交点M,N是曲线C上一动点,求|MN|的最大值 .
,(t为参数)设直线L与x轴的交点M,N是曲线C上一动点,求|MN|的最大值 .