题目内容
11.若$\overrightarrow{a}$=(2,-3,$\sqrt{3}$),$\overrightarrow{b}$=(1,0,0),则<$\overrightarrow{a}$•$\overrightarrow{b}$>=$\frac{π}{3}$.分析 根据向量的坐标运算,求出$\overrightarrow{a}$•$\overrightarrow{b}$以及|$\overrightarrow{a}$|、|$\overrightarrow{b}$|的值,计算cos<$\overrightarrow{a}$,$\overrightarrow{b}$>即可得$\overrightarrow{a}$与$\overrightarrow{b}$所成的角.
解答 解:∵$\overrightarrow{a}$=(2,-3,$\sqrt{3}$),$\overrightarrow{b}$=(1,0,0),
∴$\overrightarrow{a}$•$\overrightarrow{b}$=2×1-3×0+$\sqrt{3}$×0=2,
|$\overrightarrow{a}$|=$\sqrt{{2}^{2}{+(-3)}^{2}{+(\sqrt{3})}^{2}}$=4,
|$\overrightarrow{b}$|=$\sqrt{{1}^{2}{+0}^{2}{+0}^{2}}$=1;
∴cos<$\overrightarrow{a}$,$\overrightarrow{b}$>=$\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{a}|×|\overrightarrow{b}|}$=$\frac{2}{4×1}$=$\frac{1}{2}$,
<$\overrightarrow{a}$,$\overrightarrow{b}$>=$\frac{π}{3}$.
故答案为:$\frac{π}{3}$.
点评 本题考查了利用空间向量的坐标表示求向量所成的角的计算问题,是基础题目.

| A. | 12 | B. | 11 | C. | 10 | D. | 9 |
| A. | $\frac{8}{30}$ | B. | $\frac{7}{8}$ | C. | $\frac{1}{8}$ | D. | $\frac{7}{30}$ |
| A. | ?x0∈[0,$\frac{π}{2}$],sin x0+cos x0≥2 | B. | ?x∈(3,+∞),x2>2x+1 | ||
| C. | ?x0∈R,x02+x0=-1 | D. | ?x∈($\frac{π}{2}$,π),tan x>sin x |
| A. | 3件都是正品 | B. | 至少有1次品 | C. | 3件都是次品 | D. | 至少有1件正品 |
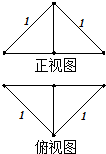 把边长为1的正方形ABCD沿对角线BD折起,形成三棱锥C-ABD,它的正视图与俯视图如图所示,则三棱锥C-ABD的体积为$\frac{\sqrt{2}}{12}$,表面积为1+$\frac{\sqrt{3}}{2}$.
把边长为1的正方形ABCD沿对角线BD折起,形成三棱锥C-ABD,它的正视图与俯视图如图所示,则三棱锥C-ABD的体积为$\frac{\sqrt{2}}{12}$,表面积为1+$\frac{\sqrt{3}}{2}$.