题目内容
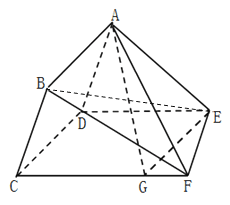
【题目】设偶函数![]() 和奇函数
和奇函数![]() 的图象如图所示,集合A
的图象如图所示,集合A ![]() 与集合B
与集合B ![]() 的元素个数分别为a,b,若
的元素个数分别为a,b,若![]() ,则a+b的值不可能是( )
,则a+b的值不可能是( )

A. 12B. 13C. 14D. 15
【答案】D
【解析】
利用f(x),g(x)图象,分别判断g(x)=t和f(x)=t,在![]() <t<1时的取值情况,进行分类讨论即可.
<t<1时的取值情况,进行分类讨论即可.
由条件知,第一个图象为f(x)的图象,第二个为g(x)的图象.
由图象可知若f(x)=0,则x有3个解,为x=﹣![]() ,x=0,x=
,x=0,x=![]() ,若g(x)=0,则x有3个解,不妨设为x=-n,x=0,x=n,(0<n<1)
,若g(x)=0,则x有3个解,不妨设为x=-n,x=0,x=n,(0<n<1)
当f(g(x)﹣t)=0得g(x)﹣t=![]() ,或g(x)﹣t=0,或g(x)﹣t=﹣
,或g(x)﹣t=0,或g(x)﹣t=﹣![]() ,.
,.
即g(x)=t+![]() ,或g(x)=t,或g(x)=t﹣
,或g(x)=t,或g(x)=t﹣![]() .
.![]()
![]() <t<1时,
<t<1时,
若g(x)=t,得x有3个解;
若g(x)=t﹣![]()
![]() ,此时x有3个解;
,此时x有3个解;
若g(x)=t+![]()
![]() ,此时方程无解.所以a=3+3=6.
,此时方程无解.所以a=3+3=6.
当g(f(x)﹣t)=0得f(x)﹣t=n,或f(x)﹣t=0或f(x)﹣t=﹣n.
即f(x)=t+n,或f(x)=t,或f(x)=t﹣n.![]()
![]() <t<1,0<n<1,
<t<1,0<n<1,
若f(x)=t,所以此时x有4个解.
若f(x)=t+n,当0<n<![]() ,则
,则![]() <t+n<
<t+n<![]() ,此时x有4个解或2解或0个解.对应f(x)=t﹣n∈(0,1)有4个解,
,此时x有4个解或2解或0个解.对应f(x)=t﹣n∈(0,1)有4个解,
此时b=4+4+4=12或b=4+2+4=10或b=4+0+4=8.
若![]() ,则1<t+n<2,此时x无解.对应f(x)=t﹣n∈(
,则1<t+n<2,此时x无解.对应f(x)=t﹣n∈(![]() ,
,![]() )有2个解或3解或4个解.
)有2个解或3解或4个解.
所以此时b=4+2=6或b=4+3=7或b=4+4=8.
综上b=12或10或8或6或7.所以a+b=18或16或14或13或12.
故选:D.

练习册系列答案
相关题目