题目内容
（2010•武汉模拟）M为△ABC内一点，过点M的一直线交AB边于P，交AC边于点Q，且满足“
+
=3”那么M一定是△ABC的（ ）
| AB |
| AP |
| AC |
| AQ |
分析：先考察两种特殊情形：当P与B重合时，当Q与C重合时，直线BM和CM都过三角形某一边的中点，再根据三角形中线段长度之间的等量关系判断出直线AM过BC边中点F，从而得出正确答案．
解答：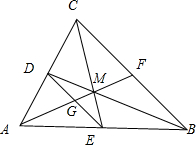
解：∵P为AB边上（除A外）的任意一点，所以当P与B重合时，
可得，
+
=3
∴
=2，
此时Q为AC边中点，
即直线BM过AC边中点．
同理，因为Q为AC边上（除A外）的任意一点
∴当Q与C重合时，可得，
+
=3，
∴
=2，此时P为AB边中点，
即直线CM过AB边中点；
设D为AC边中点，E为AB边中点，连接ED，直线AM分别交ED、BC于G、F，
∵ED是△ABC的一条中位线，
∴
=
=
∵
=
=
=
=
，
∴
=
=
，
∴BF=FC
∵BF=FC，
∴F为BC边上中点，因为直线BM过AC边中点D，直线CM过AB边中点E，直线AM过BC边中点F，
∴M为△ABC的重心．
故选A．
解：∵P为AB边上（除A外）的任意一点，所以当P与B重合时，可得，
| AB |
| AB |
| AC |
| AQ |
∴
| AC |
| AQ |
此时Q为AC边中点，
即直线BM过AC边中点．
同理，因为Q为AC边上（除A外）的任意一点
∴当Q与C重合时，可得，
| AB |
| AP |
| AC |
| AC |
∴
| AB |
| AP |
即直线CM过AB边中点；
设D为AC边中点，E为AB边中点，连接ED，直线AM分别交ED、BC于G、F，
∵ED是△ABC的一条中位线，
∴
| EG |
| BF |
| AE |
| AB |
| 1 |
| 2 |
∵
| EG |
| FC |
| EM |
| MC |
| DM |
| MB |
| ED |
| BC |
| 1 |
| 2 |
∴
| EG |
| BF |
| EG |
| FC |
| 1 |
| 2 |
∴BF=FC
∵BF=FC，
∴F为BC边上中点，因为直线BM过AC边中点D，直线CM过AB边中点E，直线AM过BC边中点F，
∴M为△ABC的重心．
故选A．
点评：本题主要考查了三角形的重心问题．解决三角形的重心问题要注意三角形的重心满足的性质：到顶点距离等于到对边中点的2倍．
练习册系列答案
相关题目