题目内容
已知偶函数 在区间
在区间 单调递减,则满足
单调递减,则满足
 的
的 取值范围是( )
取值范围是( )
A. | B. |
C. | D.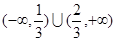 |
A
解析试题分析:∵ 在区间
在区间 单调递减,∴当
单调递减,∴当 时,即
时,即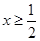 时,不等式
时,不等式
 可化为
可化为 ,解得
,解得 ,结合
,结合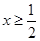 可得
可得 的取值范围是
的取值范围是 ;当
;当 时,即
时,即 时,因为函数
时,因为函数 是偶函数
是偶函数 ,∴不等式
,∴不等式
 等价于
等价于
 ,可化为
,可化为 ,解得
,解得 ,结合
,结合 可得
可得 的取值范围是
的取值范围是 ,综上
,综上 的取值范围是
的取值范围是 ,故选A.
,故选A.
考点:函数的奇偶性与单调性

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案
相关题目
下列函数在区间 是增函数的是
是增函数的是
A. | B. | C. | D. |
已知函数 ,若关于
,若关于 的方程
的方程 有两个不同的实根,则实数
有两个不同的实根,则实数 的取值范围是( )
的取值范围是( )
A. | B. | C.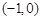 | D.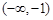 |
在区间 上不是增函数的是( )
上不是增函数的是( )
A. | B. | C. | D.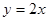 |
规定 表示不超过
表示不超过 的最大整数,
的最大整数, ,若方程
,若方程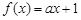 有且仅有四个实数根,则实数
有且仅有四个实数根,则实数 的取值范围是( )
的取值范围是( )
A. | B. | C. | D. |
已知偶函数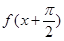 ,当
,当 时,
时, ,设
,设

 ,则( )
,则( )
A.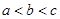 | B. | C. | D. |
下列函数中,既是奇函数又在定义域上是增函数的为
A.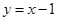 | B. | C. | D. |
若奇函数f(x)在(0,+∞)上的解析式是f(x)=x(1-x),则在(-∞,0)上,f(x)的解析式是( ).
| A.f(x)=-x(1-x) | B.f(x)=x(1+x) |
| C.f(x)=-x(1+x) | D.f(x)=x(1-x) |
 的函数,若存在距离为
的函数,若存在距离为 的两条平行直线
的两条平行直线 和
和 ,使得当
,使得当 时,
时, 恒成立,则称函数
恒成立,则称函数 在
在 ;②
;② ;③
;③ ;④
;④ .其中在
.其中在 上通道宽度为
上通道宽度为 的函数是( )
的函数是( )