题目内容
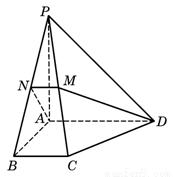
(本题满分8分)如图,已知△ABC在平面α外,它的三边所在直线分别交平面α于点P、Q、R,求证:P、Q、R三点共线.

【答案】
证明:设△ABC确定平面ABC,直线AB交平面α于点Q,直线CB交平面α于点P,直线AC交平面α于点R,则P、Q、R三点都在平面α内,
又因为P、Q、R三点都在平面ABC内,
所以P、Q、R三点都在平面α和平面ABC的交线上,而两平面的交线只有一条,所以P、Q、R三点共线.
【解析】略

练习册系列答案
相关题目
 中,
中, 是
是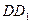 的中点,
的中点,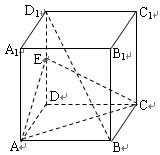
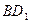 ∥平面
∥平面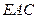 ;
;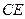 所成角的余弦值.
所成角的余弦值.
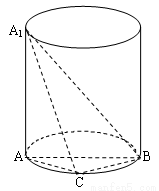
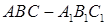 中,
中,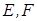 分别是
分别是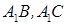 的中点,点
的中点,点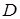 在
在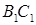 上,
上,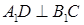
 ∥平面
∥平面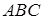
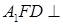 平面
平面
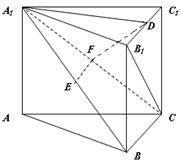
 中,底面为直角梯形,
中,底面为直角梯形,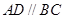 ,
,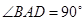 ,
,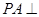 底面
底面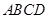 ,且
,且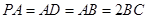 ,
,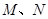 分别为
分别为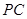 、
、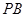 的中点。
的中点。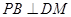 ;
;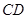 与平面
与平面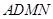 所成角的正弦值。
所成角的正弦值。