题目内容
如图,在底面是矩形的四棱锥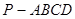 中,
中, ,
,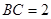 .
.
(1)求证:平面 ;
;
(2)若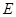 为
为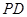 的中点,求异面直线
的中点,求异面直线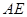 与
与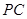 所成角的余弦值;
所成角的余弦值;
(3)在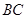 上是否存在一点
上是否存在一点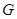 ,使得
,使得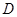 到平面
到平面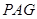 的距离为1?若存在,求出
的距离为1?若存在,求出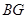 ,若不存在,请说明理由。(10分)
,若不存在,请说明理由。(10分)
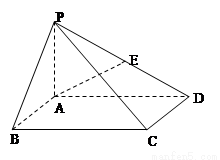
【答案】
证明:(1) 所以
所以 面
面 ,而
,而 面
面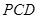 ,故平面
,故平面 平面
平面 。
(3分)
。
(3分)
(2)取 的中点
的中点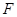 ,连接
,连接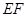 ,则
,则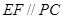 ,故
,故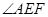 为异面直线
为异面直线 与
与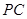 所成的角或其补角。
(4分)
所成的角或其补角。
(4分)
在三角形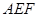 中,
中,
 ,
,
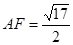 ,由余弦定理得:
,由余弦定理得:

 (6分)
(6分)
(3)因为平面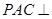 平面
平面 ,且交线为
,且交线为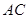 ,点
,点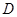 到平面
到平面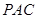 的距离小于1,故在
的距离小于1,故在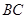 上存在一点
上存在一点 ,使得
,使得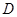 到平面
到平面 的距离为1。 (8分)
的距离为1。 (8分)
具体找法:在平面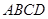 中,以
中,以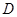 为圆心,1为半径作圆,过
为圆心,1为半径作圆,过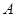 做圆的切线与
做圆的切线与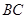 的交点便是,
的交点便是,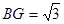 。
(10分)
。
(10分)
【解析】略

练习册系列答案
相关题目
 (2012•惠州模拟)如图,在底面是矩形的四棱锥P-ABCD中,PA⊥平面ABCD,PA=AB=2,BC=2,E是PD的中点.
(2012•惠州模拟)如图,在底面是矩形的四棱锥P-ABCD中,PA⊥平面ABCD,PA=AB=2,BC=2,E是PD的中点.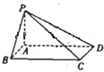 如图,在底面是矩形的四棱锥P-ABCD中,PA⊥底面ABCD,PA=AB=2,BC=4.
如图,在底面是矩形的四棱锥P-ABCD中,PA⊥底面ABCD,PA=AB=2,BC=4.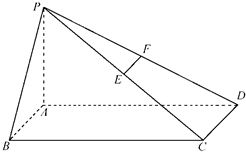 (2010•通州区一模)如图,在底面是矩形的四棱锥P-ABCD中,PA⊥底面ABCD,E、F分别是PC、PD的中点,求证:
(2010•通州区一模)如图,在底面是矩形的四棱锥P-ABCD中,PA⊥底面ABCD,E、F分别是PC、PD的中点,求证: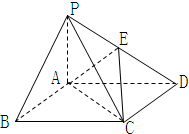 如图,在底面是矩形的四棱锥P-ABCD中,PA⊥平面ABCD,PA=AB=2,BC=4,E是PD的中点
如图,在底面是矩形的四棱锥P-ABCD中,PA⊥平面ABCD,PA=AB=2,BC=4,E是PD的中点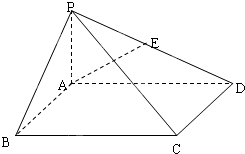 如图,在底面是矩形的四棱锥P-ABCD中,PA⊥面ABCD,PA=AB=1,BC=2.
如图,在底面是矩形的四棱锥P-ABCD中,PA⊥面ABCD,PA=AB=1,BC=2.