Question

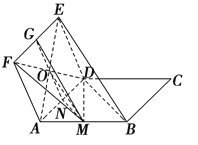
【题目】如图，ABCD与ADEF为平行四边形，M，N，G分别是AB，AD，EF的中点．求证：

（1）BE∥平面DMF；

（2）平面BDE∥平面MNG．

Answer 1

【答案】见解析

【解析】

试题分析：（1）欲证线面平行常转化为找线与面中的一条直线平行．

本题中可结合题中的中点条件，找线BE与面中的线MO平行得证．

（2）证面面平行，需运用面与面平行的判定找线与面平行，

利用中点条件找出两条相交直线DE和BD与面BDE平行得证．

试题解析：（1）如图，连接AE，则AE必过DF与GN的交点O，连接MO，

则MO为△ABE的中位线，所以BE∥MO，

又BE平面DMF，MO平面DMF，所以BE∥平面DMF．

（2）因为N，G分别为平行四边形ADEF的边AD，EF的中点，所以DE∥GN，

又DE平面MNG，GN平面MNG，所以DE∥平面MNG．

又M为AB中点，所以MN为△ABD的中位线，所以BD∥MN，

又BD平面MNG，MN平面MNG，所以BD∥平面MNG，又DE与BD为平面BDE 内的两条相交直线， 所以平面BDE∥平面MNG．