题目内容
5. 如图,BC是圆O的一条弦,延长BC至点E,使得BC=2CE,过E作圆O的切线,A为切点,∠BAC的平分线AD交BC于点D,DE=$\sqrt{3}$,则BE的长为3.
如图,BC是圆O的一条弦,延长BC至点E,使得BC=2CE,过E作圆O的切线,A为切点,∠BAC的平分线AD交BC于点D,DE=$\sqrt{3}$,则BE的长为3.
分析 利用切线的性质、角平分线的性质,证明∠ADE=∠DAE,可得AE=DE,再利用切割线定理,即可求出CE的长,即可求出BE.
解答 解:∵AE是圆O的切线,
∴∠EAC=∠B,
又∵AD是∠BAC的平分线,∴∠BAD=∠DAC.
∴∠ADE=∠DAE,
∴AE=DE,
设CE=x,
∵AE是圆O的切线,
∴AE2=CE•BE,
∵BC=2CE,∴DE2=x•3x=3,
∴x=1,
∴BE=3.
故答案为:3.
点评 本题考查切线的性质、角平分线的性质,考查切割线定理,考查学生的计算能力,比较基础.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
17.已知圆C的圆心在y轴的负半轴上,且与x轴相切,被双曲线$\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{12}$=1的渐近线截得的弦长为$\sqrt{3}$,则圆C的方程为( )
| A. | x2+(y+1)2=1 | B. | x2+(y+$\sqrt{3}$)2=3 | C. | x2+(y+$\frac{\sqrt{3}}{2}$)2=$\frac{3}{4}$ | D. | x2+(y+2)2=4 |
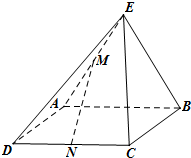 如图,矩形ABCD所在平面与直角三角形ABE所在平面互相垂直,AE⊥BE,点M,N分别是AE,CD的中点.
如图,矩形ABCD所在平面与直角三角形ABE所在平面互相垂直,AE⊥BE,点M,N分别是AE,CD的中点. 如图,AB是圆O的直径,C是半径OB的中点,D是OB延长线上一点,且BD=OB,直线MD与圆O相交于点M,T(不与A,B重合),连结MC,MB,OT.
如图,AB是圆O的直径,C是半径OB的中点,D是OB延长线上一点,且BD=OB,直线MD与圆O相交于点M,T(不与A,B重合),连结MC,MB,OT. 如图,AB是圆O的直径,点C在圆O上,延长BC到D使BC=CD,过C作圆O的切线交AD于E.若AB=8,DC=4,则DE=2.
如图,AB是圆O的直径,点C在圆O上,延长BC到D使BC=CD,过C作圆O的切线交AD于E.若AB=8,DC=4,则DE=2. 如图1,一个底面是正三角形,侧棱与底面垂直的棱柱形容器,底面边长为a,高为2a,内装水若干.将容器放倒,把一个侧面作为底面,如图2,这时水面恰好为中截面(D,D′E,E′分别是棱CB,C′B′,CA,C′A′的中点),则图1中容器内水面的高度为$\frac{3}{2}$a.
如图1,一个底面是正三角形,侧棱与底面垂直的棱柱形容器,底面边长为a,高为2a,内装水若干.将容器放倒,把一个侧面作为底面,如图2,这时水面恰好为中截面(D,D′E,E′分别是棱CB,C′B′,CA,C′A′的中点),则图1中容器内水面的高度为$\frac{3}{2}$a.