题目内容
已知二次函数f(x)=ax2+bx+c满足条件:①0,1是f(x)=0的两个零点;②f(x)的最小值为![]() .
.
(1)求函数f(x)的解析式;
(2)设数列{an}的前n项积为Tn,且Tn=λf(n)(λ≠0,n∈N*),求数列{an}的前n项和Sn;
(3)在(2)的条件下,当λ=![]() 时,若5f(an)是bn与an的等差中项,试问数列{bn}中第几项的值最小?并求出这个最小值.
时,若5f(an)是bn与an的等差中项,试问数列{bn}中第几项的值最小?并求出这个最小值.
解:(1)由题意知: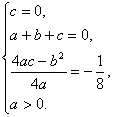
解得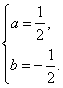 故f(x)=
故f(x)=![]() x2
x2![]() x.
x.
(2)∵Tn=a1a2…an=![]() ,当n≥2时,Tn-1=a1·a2·…·an-1=
,当n≥2时,Tn-1=a1·a2·…·an-1=![]() ,
,
∴an=![]() =λn-1(n≥2).
=λn-1(n≥2).
又a1=T1=1满足上式,∴an=λn-1(n∈N*).
当λ=1时,Sn=n,当λ≠1且λ≠0时,数列{an}是等比数列,∴Sn=![]() .
.
故数列{an}的前n项和Sn=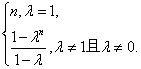
(3)若5f(an)是bn与an的等差中项,则2×5f(an)=bn+an,从而10(![]() an2
an2![]() an)=bn+an,
an)=bn+an,
得bn=5an2-6an=5(an![]() )2
)2![]() .
.
∵an=(![]() )n-1(n∈N*)是关于n的减函数,
)n-1(n∈N*)是关于n的减函数,
∴当an≥![]() ,即n≤3(n∈N*)时,bn随n的增大而减小,此时最小值为b3;
,即n≤3(n∈N*)时,bn随n的增大而减小,此时最小值为b3;
当an<![]() ,即n≥4(n∈N*)时,bn随n的增大而增大,此时最小值为b4.
,即n≥4(n∈N*)时,bn随n的增大而增大,此时最小值为b4.
又|a3![]() |<|a4
|<|a4![]() |,∴b3<b4,即数列{bn}中b3最小,
|,∴b3<b4,即数列{bn}中b3最小,
且b3=5[(![]() )2]2-6(
)2]2-6(![]() )2=
)2=![]() .
.

练习册系列答案
相关题目