题目内容

12．如图，△ABC及其内部的点组成的集合记为D，P（x，y）为D中任意一点，则z=2x+3y的最大值为7．

分析 利用线性规划的知识，通过平移即可求z的最大值．

解答 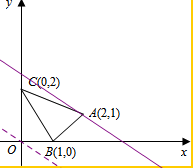解：由z=2x+3y，得y=$-\frac{2}{3}x+\frac{z}{3}$，
平移直线y=$-\frac{2}{3}x+\frac{z}{3}$，由图象可知当直线y=$-\frac{2}{3}x+\frac{z}{3}$经过点A时，直线y=$-\frac{2}{3}x+\frac{z}{3}$的截距最大，此时z最大．
即A（2，1）．
此时z的最大值为z=2×2+3×1=7，
故答案为：7．

点评 本题主要考查线性规划的应用，利用数形结合是解决线性规划题目的常用方法．

练习册系列答案
相关题目
2．设x3+ax+b=0，其中a，b均为实数，下列条件中，使得该三次方程仅有一个实根的是①③④⑤（写出所有正确条件的编号）
①a=-3，b=-3．②a=-3，b=2．③a=-3，b＞2．④a=0，b=2．⑤a=1，b=2．
3．不等式2${\;}^{{x}^{2}-x}$＜4的解集为（-1，2）．
20．不等式-x2-3x+4＞0的解集为（-4，1）．（用区间表示）
7．某辆汽车每次加油都把油箱加满，下表记录了该车相邻两次加油时的情况
加油时间加油量（升）加油时的累计里程（千米）
2015年5月1日1235000
2015年5月15日4835600
注：“累计里程”指汽车从出厂开始累计行驶的路程，在这段时间内，该车每100千米平均耗油量为 （　　）
A．6升B．8升C．10升D．12升
17．若直线3x-4y+5=0与圆x2+y2=r2（r＞0）相交于A，B两点，且∠AOB=120°，（O为坐标原点），则r=2．
4．设向量$\overrightarrow{a}$，$\overrightarrow{b}$不平行，向量λ$\overrightarrow{a}$+$\overrightarrow{b}$与$\overrightarrow{a}$+2$\overrightarrow{b}$平行，则实数λ=$\frac{1}{2}$．
1．已知A，B，C在圆x2+y2=1上运动，且AB⊥BC，若点P的坐标为（2，0），则|$\overrightarrow{PA}+\overrightarrow{PB}+\overrightarrow{PC}$|的最大值为（　　）
A．6B．7C．8D．9
2．定义：如果函数f（x）在[a，b]上存在x1，x2（a＜x1＜x2＜b）满足f′（x1）=$\frac{f（b）-f（a）}{b-a}$，f′（x2）$\frac{f（b）-f（a）}{b-a}$，则称函数f（x）是[a，b]上的“双中值函数”．已知函数f（x）=x3-x2+a是[0，a]上“双中值函数”，则实数a的取值范围是（　　）
A．（$\frac{1}{3}$，$\frac{1}{2}$）B．（0，1）C．（$\frac{1}{3}$，1）D．（$\frac{1}{2}$，1）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网