题目内容
在半径为
的球内放入大小相等的4个小球，则小球半径
的最大值为（ ）
A． | B． | C． | D． |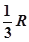
A
解析试题分析：当四个小球两两相切并且四个小球都与大球相切时，这些小球的半径最大。以四个小球球心为顶点的正四面体棱长为2r，该正四面体的中心(外接球球心)就是大球的球心，该正四面体外接球半径为
考点：空间几何体的位置关系及空间想象能力
点评：本题有一定的难度，入手点在首先分析出小球半径最大时的位置，与大球结合得到大球球心是正四面体的中心是求解的关键
练习册系列答案
相关题目
某几何体的三视图如图，则它的体积为（ ）
A． | B． | C． | D． |
一个空间几何体的三视图如右图所示，则该几何体的外接球的表面积为（ ）
A． | B． | C． | D． |
，且一个内角为60°的菱形，俯视图为正方形，那么这个几何体的表面积为
某几何体的三视图如图所示，则它的体积是（ ）
A． | B． |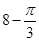
C． | D． |
用长为4，宽为2的矩形做侧面围成一个圆柱，此圆柱轴截面面积为（ ）.
| A．8 | B． | C． | D． |
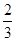
的矩形，则该正方体的正视图的面积等于（ ）
