题目内容
已知三个实数a,b,c成等比数列,且a+b+c=m(m是正常数),则b的取值范围为 .
【答案】分析:由题意可得 b2=ac,a+b+c=m,故a、c 是关于x的一元二次方程x2-(m-b)x+b2=0的两个根,由△≥0,解得b的取值范围.
解答:解:由题意可得 b2=ac,a+b+c=m,即 ,
,
∴a、c 是关于x的一元二次方程x2-(m-b)x+b2=0的两个根.
所以△=(m-b)2-4 b2≥0,解之得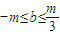 ,
,
因为b≠0,所以b的取值范围是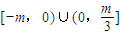 ,
,
故答案为: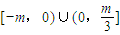 .
.
点评:本题主要考查等比数列的定义和性质,一元二次方程的根的分布与系数的关系,得到△=(m-b)2-4 b2≥0,是解题的关键.
解答:解:由题意可得 b2=ac,a+b+c=m,即
 ,
,∴a、c 是关于x的一元二次方程x2-(m-b)x+b2=0的两个根.
所以△=(m-b)2-4 b2≥0,解之得
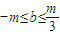 ,
,因为b≠0,所以b的取值范围是
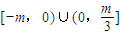 ,
,故答案为:
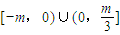 .
.点评:本题主要考查等比数列的定义和性质,一元二次方程的根的分布与系数的关系,得到△=(m-b)2-4 b2≥0,是解题的关键.

练习册系列答案
 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目