题目内容
定义在(0,+∞)的函数 ,其中e=2.71828…是自然对数的底数,a∈R.
,其中e=2.71828…是自然对数的底数,a∈R.(1)若函数f(x)在点x=1处连续,求a的值;
(2)若函数f(x)为(0,1)上的单调函数,求实数a的取值范围,并判断此时函数f(x)在(0,+∞)上是否为单调函数;
(3)当x∈(0,1)时,记g(x)=lnf(x)+x2-ax,试证明:对n∈N*,当n≥2时,有
 .
.
【答案】分析:(1)若函数f(x)在点x=1处连续,则说明当x=1时,分段函数两段函数的解析式均相等,即ea-1=1.解指数方程即可得到答案.
(2)函数f(x)为(0,1)上的单调函数,则f'(x)在区间(0,1)上恒小于0,或恒大于0,由此分类讨论后,构造关于a的不等式,解不等式即可得到答案.由此再判断f'(x)在区间(0,+∞)上的符号,即可判断函数f(x)在(0,+∞)上是否为单调函数;
(3)当x∈(0,1)时,g(x)=lnf(x)+x2-ax=lnx.则可将不等式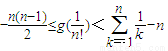 .变形为-1-2-3-^-(n-1)<ln1+ln
.变形为-1-2-3-^-(n-1)<ln1+ln +ln
+ln +…+ln
+…+ln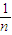 <1+
<1+ +
+ +…+
+…+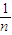 -n,分别构造函数h(t)=lnt-1+
-n,分别构造函数h(t)=lnt-1+ 与s(t)=lnt-t+1,并判断两个函数在区间(0,1)上的单调性,可得到1-
与s(t)=lnt-t+1,并判断两个函数在区间(0,1)上的单调性,可得到1- <lnt<t-1,其中t∈(0,1),代入即可证明结论.
<lnt<t-1,其中t∈(0,1),代入即可证明结论.
解答:解:(1)∵f(1)=1,,已知f(x)在点x=1处连续,
∴有ea-1=1.
∴a=1.
(2)当x∈(0,1)时,f(x)=x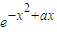
此时,f'(x)=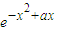 +x
+x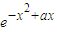 (-2x-a)=(-2x2+ax+1)
(-2x-a)=(-2x2+ax+1)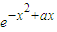 ,
,
∵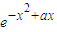 >0,
>0,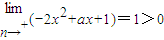 ,
,
∴f'(x)不可能在(0,1)上恒小于0.
故f(x)在(0,1)上必为增函数.
∴-2x2+ax+1 0在(0,1)上恒成立.
?a≥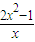 =2x-
=2x-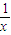 在(0,1)上恒成立.
在(0,1)上恒成立.
设u(x)=2x-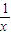 ,x∈(0,1).
,x∈(0,1).
∵u(x)在(0,1)上是增函数,u(x)<1.
∴当a≥1时,f(x)在(0,1)上是增函数.
又当a=1时,f(x)在(0,+∞)上也是增函数;
当a>1时,∵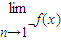 =
=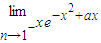 =ea-1>1=f(1),
=ea-1>1=f(1),
此时,f(x)在(0,+∞)上不是增函数.
(3)当x∈(0,1)时,g(x)=lnf(x)+x2-ax=lnx.
当n≥2时,
欲证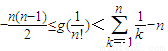 ,
,
需证:-1-2-3-^-(n-1)<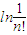 <1+
<1+ +
+ +…+
+…+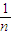 -n
-n
即需证-1-2-3-^-(n-1)<ln1+ln +ln
+ln +…+ln
+…+ln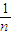 <1+
<1+ +
+ +…+
+…+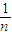 -n
-n
猜想:1- <lnt<t-1,其中t∈(0,1).
<lnt<t-1,其中t∈(0,1).
下面证明之.构造函数h(t)=lnt-1+ ,t∈(0,1).
,t∈(0,1).
∵h'(t)= -
-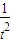 =
=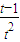 <0,
<0,
∴h(t)在(0,1)上是减函数,而,
∴h(t)>h(1)=0,即有1- <lnt
<lnt
设s(t)=lnt-t+1,t∈(0,1).
同理可证:s(t)<0,
即有1- <lnt<t-1,其中t∈(0,1).
<lnt<t-1,其中t∈(0,1).
分别取t= ,
, ,…,
,…,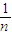 (n≥2),所以有n个不等式相加即得:
(n≥2),所以有n个不等式相加即得:
-1-2-3-^-(n-1)<ln1+ln +ln
+ln +…+ln
+…+ln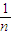 <1+
<1+ +
+ +…+
+…+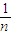 -n,
-n,
∴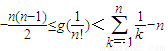
点评:利用导数研究函数的单调性比用函数单调性的定义要方便,但应注意f′(x)>0(或f′(x)<0)仅是f(x)在某个区间上为增函数(或减函数)的充分条件,在(a,b)内可导的函数f(x)在(a,b)上递增(或递减)的充要条件应是f′(x)≥0[或f′(x)≤0],x∈(a,b)恒成立,且f′(x)在(a,b)的任意子区间内都不恒等于0,这就是说,函数f(x)在区间上的增减性并不排斥在区间内个别点处有f′(x0)=0,甚至可以在无穷多个点处f′(x0)=0,只要这样的点不能充满所给区间的任何一个子区间,因此,在已知函数f(x)是增函数(或减函数)求参数的取值范围时,应令f′(x)≥0[或f′(x)≤0]恒成立,解出参数的取值范围(一般可用不等式恒成立理论求解),然后检验参数的取值能否使f′(x)恒等于0,若能恒等于0,则参数的这个值应舍去,若f′(x)不恒为0,则由f′(x)≥0[或f′(x)≤0]恒成立解出的参数的取值范围确定.
(2)函数f(x)为(0,1)上的单调函数,则f'(x)在区间(0,1)上恒小于0,或恒大于0,由此分类讨论后,构造关于a的不等式,解不等式即可得到答案.由此再判断f'(x)在区间(0,+∞)上的符号,即可判断函数f(x)在(0,+∞)上是否为单调函数;
(3)当x∈(0,1)时,g(x)=lnf(x)+x2-ax=lnx.则可将不等式
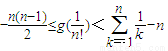 .变形为-1-2-3-^-(n-1)<ln1+ln
.变形为-1-2-3-^-(n-1)<ln1+ln +ln
+ln +…+ln
+…+ln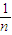 <1+
<1+ +
+ +…+
+…+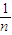 -n,分别构造函数h(t)=lnt-1+
-n,分别构造函数h(t)=lnt-1+ 与s(t)=lnt-t+1,并判断两个函数在区间(0,1)上的单调性,可得到1-
与s(t)=lnt-t+1,并判断两个函数在区间(0,1)上的单调性,可得到1- <lnt<t-1,其中t∈(0,1),代入即可证明结论.
<lnt<t-1,其中t∈(0,1),代入即可证明结论.解答:解:(1)∵f(1)=1,,已知f(x)在点x=1处连续,
∴有ea-1=1.
∴a=1.
(2)当x∈(0,1)时,f(x)=x
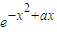
此时,f'(x)=
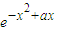 +x
+x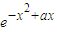 (-2x-a)=(-2x2+ax+1)
(-2x-a)=(-2x2+ax+1)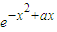 ,
,∵
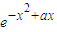 >0,
>0,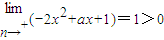 ,
,∴f'(x)不可能在(0,1)上恒小于0.
故f(x)在(0,1)上必为增函数.
∴-2x2+ax+1 0在(0,1)上恒成立.
?a≥
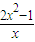 =2x-
=2x-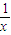 在(0,1)上恒成立.
在(0,1)上恒成立.设u(x)=2x-
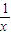 ,x∈(0,1).
,x∈(0,1).∵u(x)在(0,1)上是增函数,u(x)<1.
∴当a≥1时,f(x)在(0,1)上是增函数.
又当a=1时,f(x)在(0,+∞)上也是增函数;
当a>1时,∵
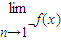 =
=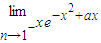 =ea-1>1=f(1),
=ea-1>1=f(1),此时,f(x)在(0,+∞)上不是增函数.
(3)当x∈(0,1)时,g(x)=lnf(x)+x2-ax=lnx.
当n≥2时,
欲证
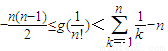 ,
,需证:-1-2-3-^-(n-1)<
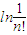 <1+
<1+ +
+ +…+
+…+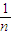 -n
-n即需证-1-2-3-^-(n-1)<ln1+ln
 +ln
+ln +…+ln
+…+ln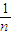 <1+
<1+ +
+ +…+
+…+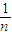 -n
-n猜想:1-
 <lnt<t-1,其中t∈(0,1).
<lnt<t-1,其中t∈(0,1).下面证明之.构造函数h(t)=lnt-1+
 ,t∈(0,1).
,t∈(0,1).∵h'(t)=
 -
-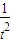 =
=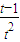 <0,
<0,∴h(t)在(0,1)上是减函数,而,
∴h(t)>h(1)=0,即有1-
 <lnt
<lnt设s(t)=lnt-t+1,t∈(0,1).
同理可证:s(t)<0,
即有1-
 <lnt<t-1,其中t∈(0,1).
<lnt<t-1,其中t∈(0,1).分别取t=
 ,
, ,…,
,…,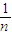 (n≥2),所以有n个不等式相加即得:
(n≥2),所以有n个不等式相加即得:-1-2-3-^-(n-1)<ln1+ln
 +ln
+ln +…+ln
+…+ln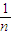 <1+
<1+ +
+ +…+
+…+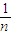 -n,
-n,∴
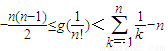
点评:利用导数研究函数的单调性比用函数单调性的定义要方便,但应注意f′(x)>0(或f′(x)<0)仅是f(x)在某个区间上为增函数(或减函数)的充分条件,在(a,b)内可导的函数f(x)在(a,b)上递增(或递减)的充要条件应是f′(x)≥0[或f′(x)≤0],x∈(a,b)恒成立,且f′(x)在(a,b)的任意子区间内都不恒等于0,这就是说,函数f(x)在区间上的增减性并不排斥在区间内个别点处有f′(x0)=0,甚至可以在无穷多个点处f′(x0)=0,只要这样的点不能充满所给区间的任何一个子区间,因此,在已知函数f(x)是增函数(或减函数)求参数的取值范围时,应令f′(x)≥0[或f′(x)≤0]恒成立,解出参数的取值范围(一般可用不等式恒成立理论求解),然后检验参数的取值能否使f′(x)恒等于0,若能恒等于0,则参数的这个值应舍去,若f′(x)不恒为0,则由f′(x)≥0[或f′(x)≤0]恒成立解出的参数的取值范围确定.

练习册系列答案
相关题目
定义在(0,+∞)上的可导函数f(x)满足f′(x)?x<f(x),且f(2)=0,则
>0的解集为( )
| f(x) |
| x |
| A、(0,2) |
| B、(0,2)∪(2,+∞) |
| C、(2,+∞) |
| D、? |