Question

（2013•浙江模拟）已知两个不重合的平面α，β，给定以下条件：
①α内不共线的三点到β的距离相等；
②l，m是α内的两条直线，且l∥β，m∥β；
③l，m是两条异面直线，且l∥α，l∥β，m∥α，m∥β；
其中可以判定α∥β的是（　　）

A．①

B．②

C．①③

D．③

Answer 1

分析：①如图1所示，平面α内的三角形ABC，边BC∥β，顶点A在β的另一侧，点M、N分别为边AB、AC的中点，且M∈α，N∈α．满足条件，但是α与β不平行；
②假设α∩β=c，l∥c，m∥c，则l∥m，满足条件，但是α与β相交不平行；
③如图3所示，过直线l作一平面γ，设γ∩α=a，γ∩β=b，过直线m作一平面π，设π∩α=c，π∩β=d，利用线面平行的性质定理和面面平行的判定定理即可判断出．

解答：解：①如图1所示，平面α内的三角形ABC，边BC∥β，顶点A在β的另一侧，点M、N分别为边AB、AC的中点，且M∈α，N∈α．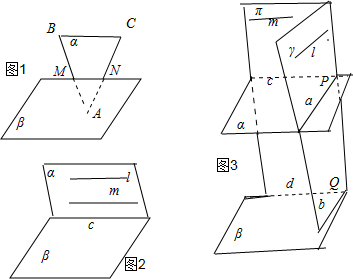
则A、B、C三点到平面β的距离相等，满足条件．但是α与β相交不平行，故不正确．
②假设α∩β=c，l∥c，m∥c，则l∥m，满足条件，但是α与β相交不平行，故不正确．
③如图3所示，过直线l作一平面γ，设γ∩α=a，γ∩β=b，∵l∥α，l∥β，则l∥a，l∥b，∴a∥β；
过直线m作一平面π，设π∩α=c，π∩β=d，∵m∥α，m∥β，则m∥c，m∥d，∴c∥β．
∵l与m是异面直线，∴a与c必定相交，∴α∥β．因此正确．
综上可知：只有③正确．
故选D．

点评：熟练掌握空间中线面、面面平行的判定与性质定理是解题的关键．