题目内容
不等式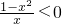 成立的一个充分不必要条件是
成立的一个充分不必要条件是
- A.-1<x<0或x>1
- B.x<-1或0<x<1
- C.x>-1
- D.x>1
D
分析:(1)首先分清条件和结论.(2)再看条件能否推出结论,结论能否推出条件.
解答:原不等式?x(x2-1)>0?-1<x<0或x>1
显然若p为不等式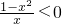 成立的一个充分不必要条件
成立的一个充分不必要条件
则:{x|P(x)}?{x|-1<x<0或x>1}
在所出答案中只有D满足要求
故选D
点评:判断充要条件的方法是:
①若p?q为真命题且q?p为假命题,则命题p是命题q的充分不必要条件;
②若p?q为假命题且q?p为真命题,则命题p是命题q的必要不充分条件;
③若p?q为真命题且q?p为真命题,则命题p是命题q的充要条件;
④若p?q为假命题且q?p为假命题,则命题p是命题q的即不充分也不必要条件.
⑤判断命题p与命题q所表示的范围,再根据“谁大谁必要,谁小谁充分”的原则,判断命题p与命题q的关系.
分析:(1)首先分清条件和结论.(2)再看条件能否推出结论,结论能否推出条件.
解答:原不等式?x(x2-1)>0?-1<x<0或x>1
显然若p为不等式
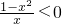 成立的一个充分不必要条件
成立的一个充分不必要条件则:{x|P(x)}?{x|-1<x<0或x>1}
在所出答案中只有D满足要求
故选D
点评:判断充要条件的方法是:
①若p?q为真命题且q?p为假命题,则命题p是命题q的充分不必要条件;
②若p?q为假命题且q?p为真命题,则命题p是命题q的必要不充分条件;
③若p?q为真命题且q?p为真命题,则命题p是命题q的充要条件;
④若p?q为假命题且q?p为假命题,则命题p是命题q的即不充分也不必要条件.
⑤判断命题p与命题q所表示的范围,再根据“谁大谁必要,谁小谁充分”的原则,判断命题p与命题q的关系.

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案
相关题目
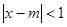 成立的一个充分不必要条件是
成立的一个充分不必要条件是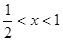 ,则实数
,则实数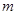 的取值范围是( )
的取值范围是( )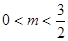 B.
B.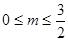 C.
C.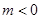 或
或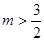 D.
D.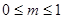
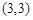 且与圆
且与圆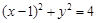 相切的直线方程为
相切的直线方程为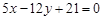 .
.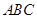 中,
中,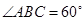 ,
,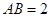 ,
,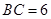 ,在
,在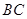 上任取一点
上任取一点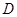 ,使△
,使△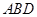 为钝角三角形的概率为
为钝角三角形的概率为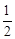
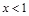 是不等式
是不等式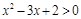 成立的一个充分不必要条件.
成立的一个充分不必要条件.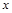 使
使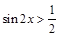 ”的否定是“存在实数
”的否定是“存在实数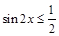 ”.
”.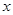 的不等式
的不等式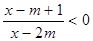 成立的一个充分非必要条件是“
成立的一个充分非必要条件是“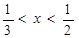 ”,则实数
”,则实数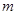 的取值范围是
.
的取值范围是
.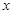 的不等式
的不等式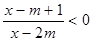 成立的一个充分非必要条件是“
成立的一个充分非必要条件是“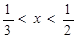 ”,则实数
”,则实数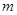 的取值范围是 .
的取值范围是 .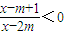 成立的一个充分非必要条件是
成立的一个充分非必要条件是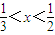 ,则实数m的取值范围是 .
,则实数m的取值范围是 .