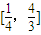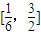题目内容
若不等式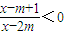 成立的一个充分非必要条件是
成立的一个充分非必要条件是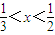 ,则实数m的取值范围是 .
,则实数m的取值范围是 .
【答案】分析:由已知中不等式 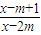 <0成立的一个充分非必要条件是
<0成立的一个充分非必要条件是  <x<
<x< ,我们分别讨论2m=m-1时,2m<m-1时,2m>m-1时满足条件的实数m的取值范围,最后综合讨论结果,即可得到答案
,我们分别讨论2m=m-1时,2m<m-1时,2m>m-1时满足条件的实数m的取值范围,最后综合讨论结果,即可得到答案
解答:解:∵设不等式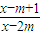 <0的解集为A
<0的解集为A
∵不等式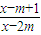 <0成立的一个充分非必要条件是
<0成立的一个充分非必要条件是  <x<
<x< ,
,
则( ,
, )?A
)?A
①当2m=m-1时,A=∅,不成立;
②当2m<m-1,即m<-1时,不等式解为A=( 2m,m-1),不符合条件,舍去;
③当2m>m-1时,不等式解为A=(m-1,2m),
则m-1≤ 且2m≥
且2m≥ ,
,
解得 ≤m≤
≤m≤ ,
,
即m取值范围是 ≤m≤
≤m≤ .
.
故答案为: ≤m≤
≤m≤
点评:本题考查的知识点是必要条件,充分条件与充要条件的判断,不等式的基本性质,其中根据已知条件分讨论,并在每种情况下构造关于m的不等式组,是解答本题的关键
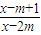 <0成立的一个充分非必要条件是
<0成立的一个充分非必要条件是  <x<
<x< ,我们分别讨论2m=m-1时,2m<m-1时,2m>m-1时满足条件的实数m的取值范围,最后综合讨论结果,即可得到答案
,我们分别讨论2m=m-1时,2m<m-1时,2m>m-1时满足条件的实数m的取值范围,最后综合讨论结果,即可得到答案解答:解:∵设不等式
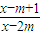 <0的解集为A
<0的解集为A∵不等式
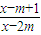 <0成立的一个充分非必要条件是
<0成立的一个充分非必要条件是  <x<
<x< ,
,则(
 ,
, )?A
)?A①当2m=m-1时,A=∅,不成立;
②当2m<m-1,即m<-1时,不等式解为A=( 2m,m-1),不符合条件,舍去;
③当2m>m-1时,不等式解为A=(m-1,2m),
则m-1≤
 且2m≥
且2m≥ ,
,解得
 ≤m≤
≤m≤ ,
,即m取值范围是
 ≤m≤
≤m≤ .
.故答案为:
 ≤m≤
≤m≤
点评:本题考查的知识点是必要条件,充分条件与充要条件的判断,不等式的基本性质,其中根据已知条件分讨论,并在每种情况下构造关于m的不等式组,是解答本题的关键

练习册系列答案
相关题目
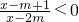 成立的一个充分非必要条件是
成立的一个充分非必要条件是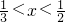 ,则实数m的取值范围是________.
,则实数m的取值范围是________.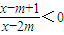 成立的一个充分非必要条件是
成立的一个充分非必要条件是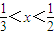 ,则实数m的取值范围是( )
,则实数m的取值范围是( )