题目内容
已知椭圆E的左右焦点分别为F1,F2,过F1作斜率为2的直线交椭圆E于P点,若△PF1F2为直角三角形,则椭圆E的离心率为 .
分析:①当PF2⊥x轴时,可得P(c,
),由于直线的斜率为2,可得
=2,即可得出.
②当PF1⊥PF2时,设|PF1|=m,|PF2|=n,则
即可得出.
| b2 |
| a |
| ||
| 2c |
②当PF1⊥PF2时,设|PF1|=m,|PF2|=n,则
|
解答:解:分类讨论:①当PF2⊥x轴时,可得P(c,
),
∵直线的斜率为2,
∴
=2,化为b2=4ac=a2-c2,
∴e2+4e-1=0,1>e>0,
解得e=
-2.
②当PF1⊥PF2时,设|PF1|=m,|PF2|=n,
则
化为9c2=5a2,
解得e=
.
综上可知:椭圆的离心率为
-2或
.
故答案为:
-2或
.
| b2 |
| a |
∵直线的斜率为2,
∴
| ||
| 2c |
∴e2+4e-1=0,1>e>0,
解得e=
| 5 |
②当PF1⊥PF2时,设|PF1|=m,|PF2|=n,
则
|
解得e=
| ||
| 3 |
综上可知:椭圆的离心率为
| 5 |
| ||
| 3 |
故答案为:
| 5 |
| ||
| 3 |
点评:本题考查了椭圆的定义与性质、分类讨论、直角三角形的边角关系等基础知识与基本技能方法,属于难题.

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
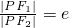 ,则e的值为________.
,则e的值为________.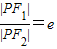 ,则e的值为 .
,则e的值为 .