题目内容
已知椭圆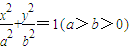 与抛物线y2=2px(p>0)有相同的焦点F,P,Q是椭圆与抛物线的交点,若PQ经过焦点F,则椭圆
与抛物线y2=2px(p>0)有相同的焦点F,P,Q是椭圆与抛物线的交点,若PQ经过焦点F,则椭圆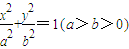 的离心率为 .
的离心率为 .
【答案】分析:先利用条件求出F,P的坐标和椭圆另一焦点坐标,进而求出|PE|,|PF|和|EF|,再利用椭圆定义求出2a和2c就可找到椭圆的离心率.
解答: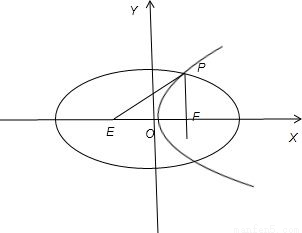 解:因为抛物线y2=2px(p>0)的焦点F为(
解:因为抛物线y2=2px(p>0)的焦点F为(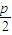 ,0),设椭圆另一焦点为E.
,0),设椭圆另一焦点为E.
当x=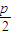 时代入抛物线方程得y=±p.又因为PQ经过焦点F,所以P(
时代入抛物线方程得y=±p.又因为PQ经过焦点F,所以P(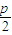 ,p)且PF⊥OF.
,p)且PF⊥OF.
所以|PE|=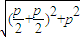 =
=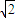 p,|PF|=P.|EF|=p.
p,|PF|=P.|EF|=p.
故2a=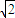 p+p,2c=p.e=
p+p,2c=p.e=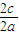 =
=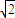 -1.
-1.
故答案为: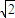 -1.
-1.
点评:本题求椭圆的离心率.在求椭圆的离心率时,一般是求出a,c,也可以求出b,c或b,a;再利用a,b,c之间的关系求a,c即可求出椭圆的离心率.
解答:
 解:因为抛物线y2=2px(p>0)的焦点F为(
解:因为抛物线y2=2px(p>0)的焦点F为(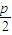 ,0),设椭圆另一焦点为E.
,0),设椭圆另一焦点为E.当x=
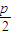 时代入抛物线方程得y=±p.又因为PQ经过焦点F,所以P(
时代入抛物线方程得y=±p.又因为PQ经过焦点F,所以P(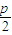 ,p)且PF⊥OF.
,p)且PF⊥OF.所以|PE|=
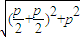 =
=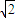 p,|PF|=P.|EF|=p.
p,|PF|=P.|EF|=p.故2a=
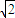 p+p,2c=p.e=
p+p,2c=p.e=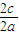 =
=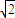 -1.
-1.故答案为:
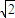 -1.
-1.点评:本题求椭圆的离心率.在求椭圆的离心率时,一般是求出a,c,也可以求出b,c或b,a;再利用a,b,c之间的关系求a,c即可求出椭圆的离心率.

练习册系列答案
相关题目
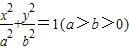 与抛物线y2=2px(p>0)有相同的焦点F,P,Q是椭圆与抛物线的交点,若PQ经过焦点F,则椭圆
与抛物线y2=2px(p>0)有相同的焦点F,P,Q是椭圆与抛物线的交点,若PQ经过焦点F,则椭圆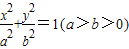 的离心率为 .
的离心率为 . 与抛物线y2=2px(p>0)有相同的焦点F,P,Q是椭圆与抛物线的交点,若PQ经过焦点F,则椭圆
与抛物线y2=2px(p>0)有相同的焦点F,P,Q是椭圆与抛物线的交点,若PQ经过焦点F,则椭圆 的离心率为 .
的离心率为 .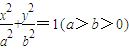 与抛物线y2=2px(p>0)有相同的焦点F,P,Q是椭圆与抛物线的交点,若PQ经过焦点F,则椭圆
与抛物线y2=2px(p>0)有相同的焦点F,P,Q是椭圆与抛物线的交点,若PQ经过焦点F,则椭圆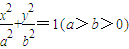 的离心率为 .
的离心率为 .