题目内容
【题目】已知函![]() ,其中
,其中![]() .
.
(Ⅰ)若![]() ,求曲线
,求曲线![]() 在点(2,f(2))处的切线方程;
在点(2,f(2))处的切线方程;
(Ⅱ)若在区间![]() 上,f(x)>0恒成立,求a的取值范围.
上,f(x)>0恒成立,求a的取值范围.
【答案】(1) y=6x-9 ;(2) 0<a<5.
【解析】
(Ⅰ)当![]() 时,代入函数的解析式求得
时,代入函数的解析式求得![]() 和
和![]() ,进而求得
,进而求得![]() ,即切线的斜率为
,即切线的斜率为![]() ,再利用直线的点斜式方程,即可求解;
,再利用直线的点斜式方程,即可求解;
(Ⅱ)求出![]() 时
时![]() 的值,分
的值,分![]() 和
和![]() 两种情况讨论函数的增减性分别取得
两种情况讨论函数的增减性分别取得![]() 和
和![]() ,及
,及![]() 和
和![]() 都大于
都大于![]() ,联立分别求解
,联立分别求解![]() 的解集,取并集,即可得到
的解集,取并集,即可得到![]() 的取值范围.
的取值范围.
(Ⅰ)解:当a=1时,f(x)=![]() ,f(2)=3;
,f(2)=3;![]() ,
, ![]() .
.
所以曲线y=f(x)在点(2,f(2))处的切线方程为y-3=6(x-2),即y=6x-9
(Ⅱ)解:![]() .令
.令![]() ,解得x=0或x=
,解得x=0或x=![]()
以下分两种情况讨论:
若![]() ,当x变化时,
,当x变化时,![]() ,
,![]() 的变化情况如下表:
的变化情况如下表:
X |
| 0 |
|
f’(x) | + | 0 | - |
f(x) |
| 极大值 |
|
当![]() 等价于
等价于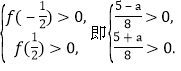
解不等式组得-5<a<5.因此![]() .
.
(2)若a>2,则![]() .当x变化时,
.当x变化时,![]() ,
,![]() 的变化情况如下表:
的变化情况如下表:
X |
| 0 |
|
|
|
f’(x) | + | 0 | - | 0 | + |
f(x) |
| 极大值 |
| 极小值 |
|
当![]() 时,f(x)>0等价于
时,f(x)>0等价于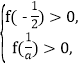 即
即
解不等式组得![]() 或
或![]() .因此2<a<5
.因此2<a<5
综合(1)和(2),可知a的取值范围为0<a<5.

 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案 新活力总动员暑系列答案
新活力总动员暑系列答案【题目】高考复习经过二轮“见多识广”之后,为了研究考前“限时抢分”强化训练次数![]() 与答题正确率
与答题正确率![]() ﹪的关系,对某校高三某班学生进行了关注统计,得到如下数据:
﹪的关系,对某校高三某班学生进行了关注统计,得到如下数据:
| 1 | 2 | 3 | 4 |
| 20 | 30 | 50 | 60 |
(1)求![]() 关于
关于![]() 的线性回归方程,并预测答题正确率是100﹪的强化训练次数;
的线性回归方程,并预测答题正确率是100﹪的强化训练次数;
(2)若用![]() 表示统计数据的“强化均值”(精确到整数),若“强化均值”的标准差在区间
表示统计数据的“强化均值”(精确到整数),若“强化均值”的标准差在区间![]() 内,则强化训练有效,请问这个班的强化训练是否有效?
内,则强化训练有效,请问这个班的强化训练是否有效?
附:回归直线的斜率和截距的最小二乘法估计公式分别为:
 ,
,![]() =
=![]() -
-![]()
![]() ,
,
样本数据![]() 的标准差为:
的标准差为: .
.
【题目】某大学准备在开学时举行一次大学一年级学生座谈会,拟邀请20名来自本校机械工程学院、海洋学院、医学院、经济学院的学生参加,各学院邀请的学生数如下表所示:
学院 | 机械工程学院 | 海洋学院 | 医学院 | 经济学院 |
人数 | 4 | 6 | 4 | 6 |
(Ⅰ)从这20名学生中随机选出3名学生发言,求这3名学生中任意两个均不属于同一学院的概率;
(Ⅱ)从这20名学生中随机选出3名学生发言,设来自医学院的学生数为ξ,求随机变量ξ的概率分布列和数学期望.