Question

【题目】已知四棱锥S—ABCD中，∠SDA＝2∠SAD＝90°，∠BAD＋∠ADC＝180°，AB＝CD，点F是线段

SA上靠近点A的一个三等分点，AC与BD相交于E．

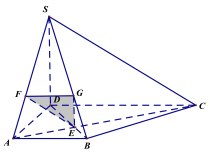
（1）在线段SB上作出点G，使得平面EFG∥平面SCD，请指明点G的具体位置，并用阴影部分表示平面EFG，不必说明平面EFG∥平面SCD的理由；

（2）若SA＝SB＝2，AB＝AD＝BD＝，求点F到平面SCD的距离．

Answer 1

【答案】（1）点G为线段SB上靠近B点的三等分点，作图见解析；（2）.

【解析】

（1）作出平面的图形如图，点G为线段SB上靠近B点的三等分点；（2）利用勾股定理得，结合可证明平面，可得平面平面，于，由此平面，即为到平面的距离，设边上的高为，则，所以.

（1）作出平面的图形如下所示，点G为线段SB上靠近B点的三等分点.

（2）依题意， 因为，故；

而，

则有，

所以，

又因为，

所以；

因为平面，

所以平面．

作于，如图，

因为平面，

所以平面；

又因为，

所以即为到平面的距离．

在△中，设边上的高为，则，

因为，

所以，

即到平面的距离为．