题目内容
掷两枚骰子,记事件A为“向上的点数之和为n”.
(1)求所有n值组成的集合;
(2)n为何值时事件A的概率P(A)最大?最大值是多少?
(3)设计一个概率为0.5的事件(不用证明)
(1)求所有n值组成的集合;
(2)n为何值时事件A的概率P(A)最大?最大值是多少?
(3)设计一个概率为0.5的事件(不用证明)
(1)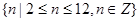
(2)n=7时候P(A)的概率最大为
(3)“向上点数和为奇数”就是其中一个概率为0.5的事件
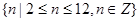
(2)n=7时候P(A)的概率最大为

(3)“向上点数和为奇数”就是其中一个概率为0.5的事件
本试题主要是考查了古典概型概率的计算的运用。
(1)掷两枚骰子,所有的情况有36种。
(2)那么利用基本事件数可知当n=7时,事件的概率最大为
(3)“向上点数和为奇数”就是其中一个概率为0.5的事件
解:(1)投掷两枚骰子的所有可能结果如下表
-----------------4分
向上的点数和有2,3,…,12,所有n值的集合为{2,3,4,5,6,7,8,9,10,11,12}
(或写成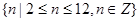 )----------6分
)----------6分
(2)由表中可见n=7时候P(A)的概率最大为 ------9分
------9分
(3)“向上点数和为奇数”就是其中一个概率为0.5的事件 -------12分
(1)掷两枚骰子,所有的情况有36种。
(2)那么利用基本事件数可知当n=7时,事件的概率最大为

(3)“向上点数和为奇数”就是其中一个概率为0.5的事件
解:(1)投掷两枚骰子的所有可能结果如下表
| | 1 | 2 | 3 | 4 | 5 | 6 |
| 1 | (1,1) | (1,2) | (1,2) | (1,4) | (1,5) | (1,6) |
| 2 | (2,1) | (2,2) | (2,3) | (2,4) | (2,5) | (2,6) |
| 3 | (3,1) | (3,2) | (3,3) | (3,4) | (3,5) | (3,6) |
| 4 | (4,1) | (4,2) | (4,3) | (4,4) | (4,5) | (4,6) |
| 5 | (5,1) | (5,2) | (5,3) | (5,4) | (5,5) | (5,6) |
| 6 | (6,1) | (6,2) | (6,3) | (6,4) | (6,5) | (6,6) |
向上的点数和有2,3,…,12,所有n值的集合为{2,3,4,5,6,7,8,9,10,11,12}
(或写成
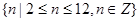 )----------6分
)----------6分(2)由表中可见n=7时候P(A)的概率最大为
 ------9分
------9分(3)“向上点数和为奇数”就是其中一个概率为0.5的事件 -------12分

练习册系列答案
相关题目
 ;②
;②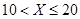 ;③
;③ ;④
;④ .调查了10000名中学生,下图是此次调查中某一项的流程图,其输出的结果是7300,则平均每人每周零花钱在
.调查了10000名中学生,下图是此次调查中某一项的流程图,其输出的结果是7300,则平均每人每周零花钱在 元内的学生的频率是( )
元内的学生的频率是( )




 分别表示甲、乙抽到的牌的数字,写出甲乙二人抽到的牌的所有情况.
分别表示甲、乙抽到的牌的数字,写出甲乙二人抽到的牌的所有情况.



 .
. ,
, )
)



 、
、 两种珍惜植物种子的发芽率进行实验性实验,每实验一次均种下一粒
两种珍惜植物种子的发芽率进行实验性实验,每实验一次均种下一粒 、
、 .假设任何两粒种子是否发芽相互之间没有影响.
.假设任何两粒种子是否发芽相互之间没有影响. ;
; ;
; ;
;