题目内容
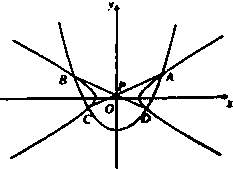 如图,双曲线
如图,双曲线| x2 | 3 |
(Ⅰ)试用m表示x1x2;
(Ⅱ)当m变化时,求p的取值范围.
分析:(Ⅰ)依题意,A、B、C、D四点坐标是下面方程组的解:
,消掉x可得y的二次方程,此时有△>0,而x可用y表示,从而用韦达定理可表示出x1x2;
(Ⅱ)由向量
=(x1,y1-p)与
=(-x2,y2-p)共线,得x1(y2-p)+x2(y1-p)=0,从而可用x1,x2表示出p,由(Ⅰ)的结论可把p用m表示出来,根据m的范围可得p的范围;
|
(Ⅱ)由向量
| PA |
| PC |
解答:解:(Ⅰ)依题意,A、B、C、D四点坐标是下面方程组的解:
消去x,得y2-y+1-m=0,
由△=1-4(1-m)>0,得m>
,且y1+y2=1,y1y2=1-m.
x1x2=
•
=3
=3
.
(Ⅱ)由向量
=(x1,y1-p)与
=(-x2,y2-p)共线,
得x1(y2-p)+x2(y1-p)=0,
∴p=
=
=
-m
=
-m=
,
∵m>
,∴0<p<
,
故p的取值范围是(0,
).
|
消去x,得y2-y+1-m=0,
由△=1-4(1-m)>0,得m>
| 3 |
| 4 |
x1x2=
| 3(y1+m) |
| 3(y2+m) |
| y1y2+m(y1+y2)+m2 |
| 1+m2 |
(Ⅱ)由向量
| PA |
| PC |
得x1(y2-p)+x2(y1-p)=0,
∴p=
| x1y2+x2y1 |
| x1+x2 |
x1(
| ||||
| x1+x2 |
| x1x2 |
| 3 |
=
| 1+m2 |
| 1 | ||
|
∵m>
| 3 |
| 4 |
| 1 |
| 2 |
故p的取值范围是(0,
| 1 |
| 2 |
点评:涉及曲线的位置关系问题,往往通过联立方程组,消元后,应用韦达定理,简化运算过程.本题(II)通过应用平面向量共线的条件,建立了p,m的关系,利用函数的观点,确定得到p的范围.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
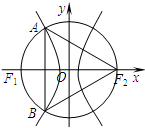 如图,F1和F2分别是双曲线
如图,F1和F2分别是双曲线