题目内容
(2013•丽水一模)已知函数f(x)=
x(1+ae-2x+2).
(Ⅰ)若a=1,记g(x)=f′(x),求证:当x>
时,0≤g(x)<
;
(Ⅱ)若x1,x2是函数f(x)的两个极值点,且x1<1<x2,若f(xi)<
(i=1,2),求实数a的取值范围.(注:e是自然对数的底数.)
| 1 |
| 2 |
(Ⅰ)若a=1,记g(x)=f′(x),求证:当x>
| 1 |
| 2 |
| 1 |
| 2 |
(Ⅱ)若x1,x2是函数f(x)的两个极值点,且x1<1<x2,若f(xi)<
| 4 |
| 3 |
分析:(Ⅰ)a=1,f(x)=
x(1+e-2x+2),可求得g(x)=f′(x),x=1时,g′(1)=0;对x分
<x<1与x>1讨论,即可证得结论;
(Ⅱ)可求得f′(xi),由f′(xi)=
+a(
-xi)e-2xi+2=0可求得e2xi-2=a(2xi-1),继而得a>0,利用(Ⅰ)的结论可求得f(xi)
[(2xi-1)+
]+
,结合已知有f(xi)<
,从而可求得xi<
或
<xi<2,再对之分类讨论,解不等式组即可.
| 1 |
| 2 |
| 1 |
| 2 |
(Ⅱ)可求得f′(xi),由f′(xi)=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2xi-1 |
| 1 |
| 2 |
| 4 |
| 3 |
| 1 |
| 2 |
| 2 |
| 3 |
解答:解(Ⅰ) 因为 a=1,所以f(x)=
x(1+e-2x+2),
g(x)=f′(x)=
x(1+e-2x+2)+
x•(-2)e-2x+2=
+(
-x)e-2x+2=,
经观察得,x=1时,g′(1)=0;
当
<x<1时,g′(x)<0,
当x>1时,g′(x)>0
所以,g(x)≥g(1)=0,又
-x<0,
所以,g(x)=
+(
-x)e-2x+2<
,
所以,当x>
时,0≤g(x)<
…(6分)
(Ⅱ) 由f′(xi)=
+a(
-xi)e-2xi+2=0
得:e2xi-2=a(2xi-1),
因为方程e2x-2=a(2x-1)有两解,所以a>0
由f(xi)=
xi(1+ae-2xi+2)=
xi(1+
)=
[(2xi-1)+
]+
<
,
解得:xi<
或
<xi<2,
(ⅰ) 当x1<
,1<x2<2时,
⇒无解
(ⅱ) 当
<x1<1,1<x2<2时,
解得1<a<3e-
,
所以,实数a的取值范围为(1,3e-
) …(14分)
| 1 |
| 2 |
g(x)=f′(x)=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
经观察得,x=1时,g′(1)=0;
当
| 1 |
| 2 |
当x>1时,g′(x)>0
所以,g(x)≥g(1)=0,又
| 1 |
| 2 |
所以,g(x)=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
所以,当x>
| 1 |
| 2 |
| 1 |
| 2 |
(Ⅱ) 由f′(xi)=
| 1 |
| 2 |
| 1 |
| 2 |
得:e2xi-2=a(2xi-1),
因为方程e2x-2=a(2x-1)有两解,所以a>0
由f(xi)=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2xi-1 |
| 1 |
| 4 |
| 1 |
| 2xi-1 |
| 1 |
| 2 |
| 4 |
| 3 |
解得:xi<
| 1 |
| 2 |
| 2 |
| 3 |
(ⅰ) 当x1<
| 1 |
| 2 |
|
(ⅱ) 当
| 2 |
| 3 |
|
| 2 |
| 3 |
所以,实数a的取值范围为(1,3e-
| 2 |
| 3 |
点评:本题考查利用导数研究函数的极值,利用导数研究函数的单调性,考查抽象思维与创新意识,考查转化思想与分类讨论思想的运用,属于难题.

练习册系列答案
相关题目
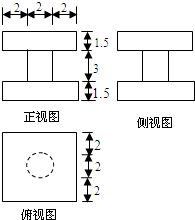 (2013•丽水一模)某几何体的三视图如图所示,则该几何体的体积为
(2013•丽水一模)某几何体的三视图如图所示,则该几何体的体积为 (2013•丽水一模)已知抛物线的顶点在坐标原点,焦点在y轴上,且过点(2,1),
(2013•丽水一模)已知抛物线的顶点在坐标原点,焦点在y轴上,且过点(2,1),