题目内容
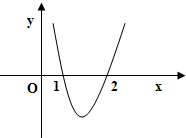 已知f(x)=ax3+bx2+cx(a≠0)有极大值5,其导函数y=f′(x)的图象如图所示,则f(x)的解析式为________.
已知f(x)=ax3+bx2+cx(a≠0)有极大值5,其导函数y=f′(x)的图象如图所示,则f(x)的解析式为________.
f(x)=2x3-9x2+12x
分析:由导函数y=f′(x)的图象可知:1,2是导函数f′(x)的零点,并且当x=1时,函数f (x)取得极大值,据此可求出答案.
解答:由f(x)=ax3+bx2+cx(a≠0),∴f′(x)=3ax2+2bx+c.
由导函数y=f′(x)的图象可知:当x<1时,f′(x)>0;当x=1时,f′(1)=0;当1<x<2时,f′(x)<0.
∴函数f(x)在x=1时取得极大值5,∴f(1)=5.
又由图象可知,1,2是导函数f′(x)的零点.
由上可得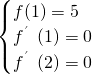 ,即
,即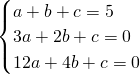 解得
解得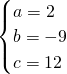 .
.
∴f(x)=2x3-9x2+12x.
故答案为f(x)=2x3-9x2+12x.
点评:本题考查了函数的极值和导函数的性质,理解函数满足什么条件时取得极值和如何利用图象是解决问题的关键.
分析:由导函数y=f′(x)的图象可知:1,2是导函数f′(x)的零点,并且当x=1时,函数f (x)取得极大值,据此可求出答案.
解答:由f(x)=ax3+bx2+cx(a≠0),∴f′(x)=3ax2+2bx+c.
由导函数y=f′(x)的图象可知:当x<1时,f′(x)>0;当x=1时,f′(1)=0;当1<x<2时,f′(x)<0.
∴函数f(x)在x=1时取得极大值5,∴f(1)=5.
又由图象可知,1,2是导函数f′(x)的零点.
由上可得
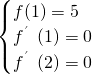 ,即
,即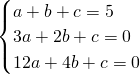 解得
解得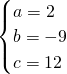 .
.∴f(x)=2x3-9x2+12x.
故答案为f(x)=2x3-9x2+12x.
点评:本题考查了函数的极值和导函数的性质,理解函数满足什么条件时取得极值和如何利用图象是解决问题的关键.

练习册系列答案
相关题目
已知F(x)=ax3+bx5+cx3+dx-6,F(-2)=10,则F(2)的值为( )
| A、-22 | B、10 | C、-10 | D、22 |