题目内容
设p:实数x满足x2-4ax+3a2<0,其中a<0,q:实数x满足x2-x-6≤0,或x2+2x-8>0,且綈p是綈q的必要不充分条件,求a的取值范围.
将必要不充分条件转化为集合之间的包含关系,从而列出a所满足的不等式而求解.
设A={x|p}={x|x2-4ax+3a2<0(a<0)}
={x|3a<x<a(a<0)};
B={x|q}={x|x2-x-6≤0或x2+2x-8>0}
={x|x2-x-6≤0}∪{x|x2+2x-8>0}
={x|-2≤x≤3}∪{x|x<-4或x>2}
={x|x<-4,或x≥-2}.
∵綈p是綈q的必要不充分条件,
∴綈q⇒綈p,且綈p⇒/綈q,
则{x|綈q}?{x|綈p}.
而{x|綈q}=∁RB={x|-4≤x<-2},
{x|綈p}=∁RA={x|x≤3a,或x≥a(a<0)},
∴{x|-4≤x<-2}?{x|x≤3a,或x≥a(a<0)},
则或即-≤a<0或a≤-4
设A={x|p}={x|x2-4ax+3a2<0(a<0)}
={x|3a<x<a(a<0)};
B={x|q}={x|x2-x-6≤0或x2+2x-8>0}
={x|x2-x-6≤0}∪{x|x2+2x-8>0}
={x|-2≤x≤3}∪{x|x<-4或x>2}
={x|x<-4,或x≥-2}.
∵綈p是綈q的必要不充分条件,
∴綈q⇒綈p,且綈p⇒/綈q,
则{x|綈q}?{x|綈p}.
而{x|綈q}=∁RB={x|-4≤x<-2},
{x|綈p}=∁RA={x|x≤3a,或x≥a(a<0)},
∴{x|-4≤x<-2}?{x|x≤3a,或x≥a(a<0)},
则或即-≤a<0或a≤-4
略

练习册系列答案
 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
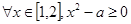 ,命题Q:
,命题Q: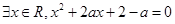
 若 “P且Q"为真命题,则实数
若 “P且Q"为真命题,则实数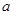 的取值范围是( )
的取值范围是( )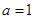 或
或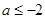 B.
B.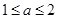 C.
C.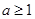 D.
D.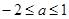
 ,有下面四个命题:
,有下面四个命题: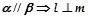 ; (2)
; (2)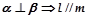 ;
; 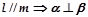 ; (4)
; (4)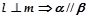 .
.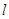
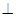 平面
平面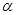 ,直线
,直线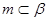 ,有如下四个命题:①
,有如下四个命题:①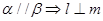 ,②
,②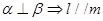 ,③
,③ ,④
,④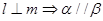 ,其中正确的命题是( )
,其中正确的命题是( )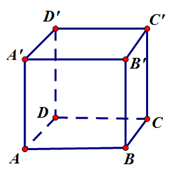
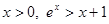 ”的否定是( )
”的否定是( )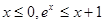
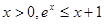
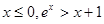
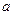 与平面
与平面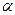 不平行,则
不平行,则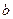 不垂直,则过
不垂直,则过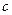 共面,则
共面,则 .2 D.3
.2 D.3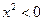 ”是不可能事件
”是不可能事件 3
3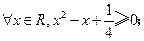
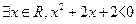 ;
;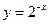 是单调递增函数.
是单调递增函数.
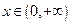 ,使得
,使得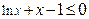 成立”的否定是_____
成立”的否定是_____ ___
___