题目内容
12.△ABC中,BC=4,AB=2AC,则S△ABC的最大值为$\frac{16}{3}$.分析 设AC=x,则AB=2x,根据面积公式得S△ABC=2x$\sqrt{1-co{s}^{2}C}$,由余弦定理求得 cosC代入化简 S△ABC=$\sqrt{\frac{256}{9}-\frac{9}{16}({x}^{2}-\frac{80}{9})^{2}}$,由三角形三边关系求得$\frac{4}{3}<x<4$,由二次函数的性质求得S△ABC取得最大值.
解答 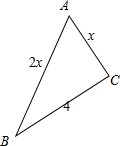 解:设AC=x,则AB=2x,根据面积公式得:S△ABC=$\frac{1}{2}$AC•BC•sinC=2x•sinC
解:设AC=x,则AB=2x,根据面积公式得:S△ABC=$\frac{1}{2}$AC•BC•sinC=2x•sinC
=2x$\sqrt{1-co{s}^{2}C}$.
由余弦定理可得:cosC=$\frac{16-3{x}^{2}}{8x}$,
∴S△ABC=2x$\sqrt{1-co{s}^{2}C}$=2x$\sqrt{1-(\frac{16-3{x}^{2}}{8x})^{2}}$=$\sqrt{-16-\frac{9}{16}{x}^{4}+10{x}^{2}}$
=$\sqrt{-\frac{9}{16}[({x}^{2}-\frac{80}{9})^{2}-\frac{4096}{81}]}$=$\sqrt{\frac{256}{9}-\frac{9}{16}({x}^{2}-\frac{80}{9})^{2}}$.
由三角形三边关系有 $\left\{\begin{array}{l}{2x+x>4}\\{x+4>2x}\end{array}\right.$,解得$\frac{4}{3}<x<4$,
故当x=$\frac{4\sqrt{5}}{3}$时,S△ABC取得最大值$\frac{16}{3}$,
故答案为:$\frac{16}{3}$.
点评 本题主要考查了余弦定理和面积公式在解三角形中的应用,考查了二次函数的性质,考查了计算能力,当涉及最值问题时,可考虑用函数的单调性和定义域等问题,属于中档题.

| A. | {1} | B. | {2} | C. | {3} | D. | {0} |
| A. | y=lg$\frac{1-x}{1+x}$ | B. | y=log2|x| | C. | y=$\frac{{e}^{x}-{e}^{-x}}{2}$ | D. | y=x2+1 |
| A. | (-∞,1] | B. | [1,2) | C. | [1,2] | D. | [3,+∞) |