题目内容
甲乙两公司生产同一种新产品,经测算,对于函数![]() ,
,![]() ,及任意的
,及任意的![]() ,当甲公司投入
,当甲公司投入![]() 万元作宣传时,乙公司投入的宣传费若小于
万元作宣传时,乙公司投入的宣传费若小于![]() 万元,则乙公司有失败的危险,否则无失败的危险;当乙公司投入
万元,则乙公司有失败的危险,否则无失败的危险;当乙公司投入![]() 万元作宣传时,甲公司投入的宣传费若小于
万元作宣传时,甲公司投入的宣传费若小于![]() 万元,则甲公司有失败的危险,否则无失败的危险. 设甲公司投入宣传费x万元,乙公司投入宣传费y万元,建立如图直角坐标系,试回答以下问题:
万元,则甲公司有失败的危险,否则无失败的危险. 设甲公司投入宣传费x万元,乙公司投入宣传费y万元,建立如图直角坐标系,试回答以下问题:
(1)请解释![]() ;
;
(2)甲、乙两公司在均无失败危险的情况下尽可能少地投入宣传费用,问此时各应投入多少宣传费?
(3)若甲、乙分别在上述策略下,为确保无失败的危险,根据对方所投入的宣传费,按最少投入费用原则,投入自己的宣传费:若甲先投入![]() 万元,乙在上述策略下,投入最少费用
万元,乙在上述策略下,投入最少费用![]() ;而甲根据乙的情况,调整宣传费为
;而甲根据乙的情况,调整宣传费为![]() ;同样,乙再根据甲的情况,调整宣传费为
;同样,乙再根据甲的情况,调整宣传费为![]()
![]() 如此得当甲调整宣传费为
如此得当甲调整宣传费为![]() 时,乙调整宣传费为
时,乙调整宣传费为![]() ;试问是否存在
;试问是否存在![]() ,
,![]() 的值,若存在写出此极限值(不必证明),若不存在,说明理由.
的值,若存在写出此极限值(不必证明),若不存在,说明理由.
⑴![]() =8,
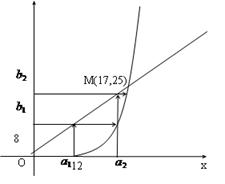
=8,![]() =12,⑵甲公司至少投入17万元,乙公司至少投入25万元.⑶点M (17, 25) 是双方在宣传投入上保证自己不失败的一个平衡点.
=12,⑵甲公司至少投入17万元,乙公司至少投入25万元.⑶点M (17, 25) 是双方在宣传投入上保证自己不失败的一个平衡点.
解析:
(1)![]() 表示当甲公司不投入宣传费时,乙公司要回避失败风险,至少要投入
表示当甲公司不投入宣传费时,乙公司要回避失败风险,至少要投入![]() =8万元; …………………… (2分)
=8万元; …………………… (2分)
![]() 表示当乙公司不投入宣传费时, 甲公司要回避失败风险,至少要投入
表示当乙公司不投入宣传费时, 甲公司要回避失败风险,至少要投入 ![]() =12万元. …………………………… (4分)
=12万元. …………………………… (4分)
(2) 解方程组
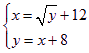 ………………(6分)
………………(6分)
得: x = 17, y = 25 ……………(9分)
故甲公司至少投入17万元,乙公司至少投入25万元. …… (11分)
(3) 经观察, 显见 ![]() .
.
故点M (17, 25) 是双方在宣传投入上保证自己不失败的一个平衡点. ………(16分)

 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 、
、 及任意的
及任意的 ,当甲公司投放
,当甲公司投放 万元改造设备时,若乙公司投放改造设备费用小于
万元改造设备时,若乙公司投放改造设备费用小于 、
、 的实际意义;
的实际意义; ,
, ,甲、乙公司为了避免恶性竞争,经过协商,同意在双方均无倒闭风险的情况下尽可能地减少改造设备资金。那么,甲、乙两公司至少各投入多少万元?
,甲、乙公司为了避免恶性竞争,经过协商,同意在双方均无倒闭风险的情况下尽可能地减少改造设备资金。那么,甲、乙两公司至少各投入多少万元?